Это интересно

Если мы хотим построить характеристики среза того вида, который соответствует фиг. 351, то для различных типов усилителей нам придется пользоваться несколько различными методами. Возможности, которые имеются в этом отношении, будут рассмотрены в этой главе несколько ниже. В следующей главе будут приведены примеры, подробно иллюстрирующие методы проектирования. Однако возможно сделать одно замечание общего характера, которое может быть отнесено к громадному большинству случаев проектирования усилителей. Если в усилителе, выполненном наиболее простым путем, без учета формы характеристики среза, мы имеем горизонтальную характеристику обратной связи в пределах рабочей полосы, то эта форма характеристики будет иметь тенденцию сохраниться и в некоторой области за пределами полосы. Такое положение имеет место, во всяком случае, для некоторой части схем. Однако на высоких частотах характеристика имеет спад за счет влияния паразитных элементов схемы. По мере повышения частоты паразитные параметры сказываются все более заметным образом, причем в конце концов общая характеристика петли обратной связи принимает асимптотический вид. В этом случае характеристика любой схемы полностью определяется только одними паразитными элементами. Таким образом, полная характеристика петли обратной связи имеет вогнутость во внутрь, если не во всей области среза, то, во всяком случае, на высоких частотах. В то же время характеристика среза, изображенная на фиг. 351, имеет вогнутость наружу. Следовательно, основная задача при проектировании большей части усилителей заключается в том, чтобы в петлю обратной связи внести такие потери, чтобы степень среза возрастала на частотах, незначительно отклоняющихся от частот рабочей полосы, и в то же время уменьшалось бы на более высоких частотах. Это эквивалентно такому уменьшению влияния паразитных параметров, при котором они уже не сказываются на характеристике петли обратной связи до тех пор, пока эта характеристика не пересекается с асимптотой.
    В качестве крайнего случая рассмотрим схему, изображенную на фиг. 355. Предполагается, что система представляет собой простой полосовой усилитель, в котором во входной и выходной цепях, а также в качестве межкаскадных элементов используются зашунтированные сопротивлениями резонансные контуры. Примем, что все контуры имеют одинаковую величину Q. Если воспользоваться соотношениями для фильтров нижних частот, то уравнение для характеристики петли можно записать как 140 (1+0,287iω)4. Коэффициенты в этом выражении выбраны таким образом, чтобы было удобно вести сравнение с результатами, приведенными на фиг. 351. Здесь получается такая же величина усиления на нижних частотах и та же асимптота, что и на указанной фигуре. Характеристика усиления петли для рассматриваемого устройства изображена в виде кривой I на фиг. 356, а теоретическая характеристика среза фиг. 351 дана кривой II. Таким образом, разность между этими кривыми, показанная в виде заштрихованной площади/соответствует величине потерь, которые должны быть внесены в петлю обратной связи с помощью выравнивающих контуров или же каких-либо аналогичных устройств с тем, чтобы стабилизировать схему.
    Результаты, которые при этом получаются, можно усмотреть на основании сравнения фазовых характеристик, показанных в виде кривых I и II фиг. 357. Площади, ограниченные этими кривыми, равны между собой, однако внесение дополнительных потерь приводит к такому перераспределению общей площади, что максимальная величина фазового сдвига остается меньше 180° в более широком интервале частот. Из чертежа видно, что исходная фазовая характеристика пересекает линию 180° на частоте f=3,5f0. Если схема стабилизирована введением регулировки усиления, с помощью которой в этой точке усиление канала уменьшено до нуля, то результирующая величина обратной связи в пределах рабочей полосы будет равна 12 дБ. Для теоретических характеристик среза соответствующая величина равна 43 дБ. Примерно половину от разности в 30 дБ для дополнительной обратной связи можно получить, если на фиг. 356 заменить кривую I прямой линией с соответствующим образом подобранной крутизной. Увеличение крутизны теоретической характеристики непосредственно за краем рабочей полосы соответствует приращению на 12 дБ, а для горизонтальной части результирующей кривой непосредственно перед пересечением с асимптотой — приращению на 5 или 6 дБ. Далее вопросы расчета, относящиеся к подобным случаям, рассмотрены более подробно.
    Анализ, который был сейчас приведен, дает возможность сделать некоторые дополнительные, в высшей степени важные, заключения. Они относятся к эффективной ширине полосы усилителей с обратной связью. Предположим, что мы приняли соотношения, приведенные на фиг. 353, как типовые для случаев практического проектирования. Тогда можно заметить, что выраженный в октавах интервал частот, лежащий в пределах между краем рабочей полосы и частотой, для которой характеристика среза пересекает линию нулевого усиления, будет на одну октаву меньше, чем величина обратной связи, выраженная в условных единицах, причем за условную единицу выбрана обратная связь в 10 дБ.
    Между точкой пересечения нулевого усиления и точкой пересечения характеристики с асимптотой имеется дополнительный интервал примерно в две октавы. Таким образом, эффективная расчетная полоса равна примерно одной октаве на каждые 10 дБ величины обратной связи плюс одна дополнительная октава. Если предполагается наличие изменений величины запаса по фазовому сдвигу и величины усиления или величины асимптотической крутизны, то это обстоятельство, хотя оно и может иметь известное значение, не вызовет, однако, изменений в смысле порядка получающихся результатов.
    Если мы будем исходить из номинальных величин, то эта значит, что усилитель с обратной связью в 30 дБ будет иметь эффективную полосу, которая на 4 октавы, т. е. в 16 раз, шире рабочей полосы. Если мы увеличим обратную связь до 60 дБ, то эффективная полоса окажется более чем в ста раз шире рабочей полосы. При рабочей полосе, которая сама по себе достаточно широка, мы придем к огромным значениям эффективной полосы. Например, для телевизионного усилителя с полосой в 4 МГц эффективная полоса при обратной связи в 30 дБ будет равна 60 МГц или 400 МГц, если мы возьмем обратную связь в 60 дБ.
    Значение полученных результатов с точки зрения инженерной практики очевидно. Они превращают проектировочный расчет усилителя с обратной связью в значительно более действенное средство, чем в том случае, когда принимается во внимание одна только ширина полосы. Выполнение и налаживание устройства, которое будет иметь заданные характеристики в столь широкой полосе частот, является, по всей вероятности, значительно более трудной задачей, чем выполнение соответствующего расчета.
    Далее...

Характеристики среза в области высоких частот

Напомним, что когда мы рассматривали вопрос о теоретических характеристиках петли для усилителей с обратной связью, то начинали с построения идеальной характеристики, которая простиралась от края рабочей полосы до бесконечности и имела заданную постоянную характеристику фазового сдвига в пределах всей этой области. Однако для получения решения, пригодного для использования на практике, необходимо принять во внимание, что характеристика петли для реальных усилителей в области достаточно высоких частот в большей степени соответствует асимптотической линии, определяемой паразитными элементами, чем идеальной характеристике.

Построение, приведенное на фиг. 351 и 353, заключалось в том, что идеальная характеристика и асимптота были соединены прямолинейным отрезком определенной длины. Такое решение вопроса является простейшим. Однако имеются другие пути к тому, чтобы соединить эти две характеристики, причем в некоторых случаях удается получить насколько большую величину допустимой обратной связи, чем для указанного выше ступенчатого построения. Поэтому утверждение о том, что величина А_т, входящая в соотношение (18.7), определяет максимально возможную величину обратной связи, не является достаточно точным. Но с точки зрения практики, дополнительные возможные решения не должны серьезно приниматься в расчет, так как они дают величину обратной связи лишь на несколько децибел большую, чем в обычных случаях. Кроме того, подбор требуемых данных затрудняется тем, что мы имеем дело с областью частот, в которой паразитные элементы схемы приобретают существенное значение. Однако возможность получения этих решений представляет принципиальный интерес л имеет известное практическое значение, как мера того, насколько точно может быть осуществлена ступенчатая характеристика с целью получения удовлетворительных результатов.

Фиг. 358

Причины возможности получения лучших результатов, чем в случае ступенчатой кривой, ясны из рассмотрения соответствующей фазовой характеристики. Из теории, относящейся к фазовому интегралу, следует, что разность между усилением по петле для некоторой достаточно низкой частоты, лежащей в пределах полосы, и усилением по петле для некоторой достаточно высокой частоты, для которой мы можем считать, что асимптотические условия целиком выполняются, — определяется площадью, ограниченной фазовой характеристикой для области, лежащей между этими двумя точками. Поэтому можно получить небольшое улучшение по сравнению со ступенчатой характеристикой среза, если заменить фазовую характеристику фиг. 352 такой, которая по возможности точно совпадает с линией 180° до края полосы и затем резко возрастает до своего конечного значения.

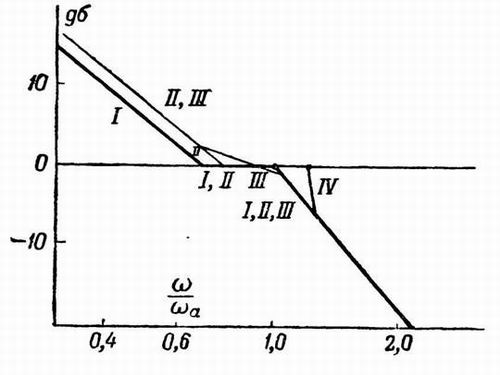
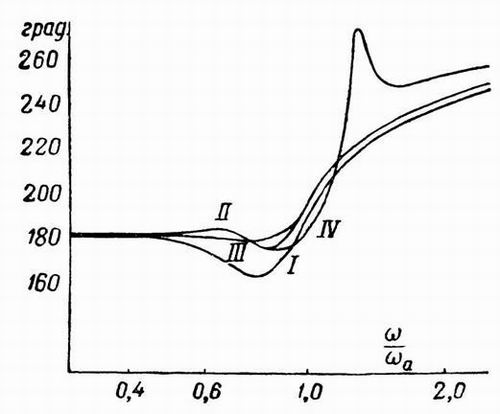
Эту задачу можно решить либо аналитически, либо путем подбора формы ступенчатой характеристики. Пример возможных вариантов подбора характеристик приведен на кривых усиления фиг. 353 и на соответствующих фазовых кривых фиг. 359. Эти кривые построены только для области, лежащей в пределах между характеристикой идеального среза и асимптотой. На обеих фигурах кривые I относятся к исходной ступенчатой характеристике, в то время как остальные кривые представляют собой видоизмененные характеристики. При построении кривых было принято для простоты, что обратная связь на нижних частотах для всех видоизмененных характеристик одна и та же, и на 2 дБ больше, чем для исходной характеристики. Указанная величина соответствует примерно тому максимальному улучшению, которое может быть достигнуто для рассматриваемого случая, для которого крутизна асимптоты равна трем условным единицам. Однако несколько большая величина выигрыша может быть получена при больших значениях n. Наиболее простой из видоизмененных характеристик является кривая II, полученная путем некоторого удлинения горизонтальной части исходной характеристики.

Влияние, которое оказывает приближение фазовой характеристики к линии 180° в области, близкой к краю полосы, можно уяснить из рассмотрения фазовых характеристик фиг. 359. Строго говоря, этот вид характеристики не может быть отнесен к абсолютно устойчивым усилителям, так как здесь на нижних частотах получается фазовый сдвиг, несколько больший 180°. Однако величина этого превышения, очевидно, невелика и ею можно пренебречь, если принять во внимание, что усилители выполняются с известным запасом по фазовому сдвигу. Поэтому А_т представляет интерес лишь как одна из величин, которая входит в соотношение (18.9).

Фиг. 359

Кривая III получена путем замены горизонтальной ступеньки исходной характеристики линией, имеющей небольшой наклон. За исключением того, что здесь затруднения с фазовой характеристикой в области нижних частот оказываются обойденными, в остальных отношениях мы получаем результаты, аналогичные предыдущему случаю. Однако в связи с тем, что точно контролировать характеристики петли обратной связи в асимптотической области довольно затруднительно, эти кривые дают результаты, которые могут быть получены легче, чем в случае кривых вида I или II. Кривые IV приведены для того, чтобы показать, каким образом повлияет продление плоской ступеньки характеристики до точки пересечения с асимптотой. Можно представить, что подобная характеристика получена за счет применения в какой-то части канала противорезонансного контура, включающего в себя паразитную емкость. Согласно расчету, подобный метод позволяет значительно увеличить допустимую обратную связь в том случае, если продолжение характеристики идет достаточно далеко, например, вплоть до частот, которые в 10 раз выше частоты, соответствующей точке пересечения асимптоты с линией нулевого усиления. Однако очевидно, что таким соотношениям будет соответствовать неосуществимая величина обратной связи на верхних частотах. В качестве более непосредственной причины, которая может привести к ограничениям, отметим то обстоятельство, что, по мере того как горизонтальная часть характеристики будет продолжена в область все более и более высоких частот, максимальная величина фазового сдвига будет становиться все значительнее. В то же время, если рассматривать петлю как цепь, в которую входят п реактивных ветвей, включенных последовательно или параллельно, то максимальная величина фазового сдвига, которая может быть физически осуществлена, будет равна n(π/2) радиан. Этот предел несколько выше того, который можно получить даже при использовании соотношений соответствующих кривых фиг. 358 и 359.

Несколько .более систематический подход к указанной общей задаче может быть получен, если мы будем добиваться, чтобы фазовая характеристика точно проходила через все заданные точки за пределами рабочей полосы. При этом для асимптотического случая предполагается, что для очень высоких частот величина фазового сдвига равна n(π/2) радиан. Соответствующие характеристики усиления могут быть определены с помощью общих формул. В качестве одного из примеров результатов, которые могут быть получены таким путем, можно привести соотношение

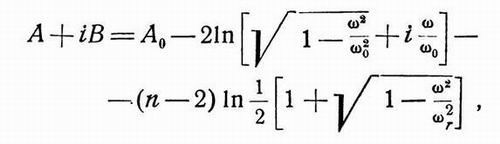(18.10)

где так же, как и в (18.1), А и В определяют усиление и величину фазового сдвига для петли, а А₀ есть усиление по петле в пределах рабочей полосы.

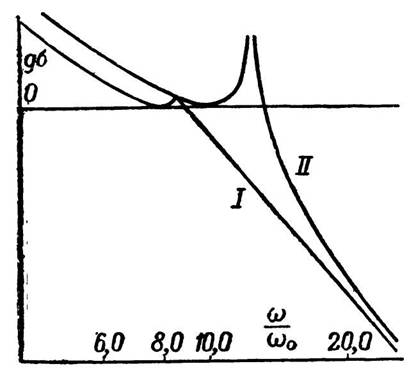
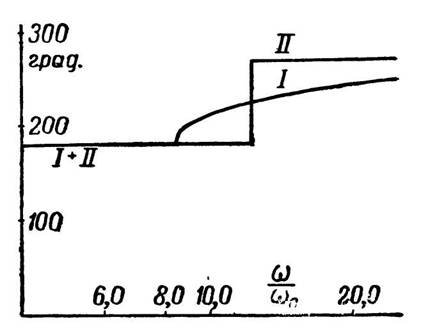
Характеристики А и В для случая уравнения (18.10) обозначены цифрой I на фиг. 360 и 361.

В качестве второго примера приведем соотношение

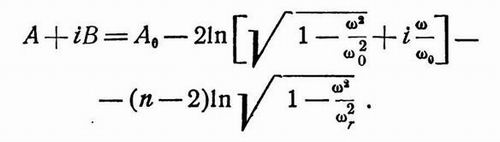(18.11)

Характеристики для А и В в данном случае даются кривыми II на фиг. 360 и 361. Из приведенных результатов видно, что оба выражения дают качественно сходные по своему виду характеристики, но имеющееся различие в форме этих характеристик особенно заметно в случае фиг. 361.

Смысл соотношений (18.10) и (18.11) можно понять лучше, если сравнить их с (18.1). Очевидно, что первая часть обоих выражений определяет решение, соответствующее идеальному срезу для предельного случая нулевого запаса по фазовому сдвигу. Последние члены обоих выражений представляют собой "переходные члены", определяющие переход от решения для идеального среза на высоких частотах к асимптотической характеристике. Таким образом, ни один из этих членов не оказывает заметного влияния на усиление петли в пределах рабочей полосы и не изменяет величину фазового сдвига на частотах ниже f_r. Эта частота соответствует точке острого угла характеристики для кривой I фиг. 360 или пику характеристики II. С другой стороны, на частотах, которые значительно выше f_r, последние члены вызывают фазовый сдвиг в (п — 2)(π/2) радиан и наклон характеристики с крутизной в (п — 2) условных единиц. В сочетании с величиной фазового сдвига и наклоном характеристики для случая идеального среза это дает крутизну в п условных единиц и фазовый сдвиг в п(π/2) радиан, что соответствует данным асимптотической характеристики.

Фиг. 360

Фиг. 361

Если мы выберем частоту f_r и величину обратной связи в пределах рабочей полосы таким образом, чтобы удовлетворить двум указанным ниже условиям, то рассматриваемые выражения получат определенное численное значение. Очевидно, что первое условие заключается в том, что уравнения должны определять собой асимптоту, соответствующую необходимому уровню абсолютного усиления, а также необходимой величине крутизны характеристики. Второе условие предполагает, что для каждой из характеристик усиления, наступающий непосредственно за частотой f_r минимум обусловливает спад характеристики до уровня нулевой линии усиления.

Фиг. 362

Фиг. 363

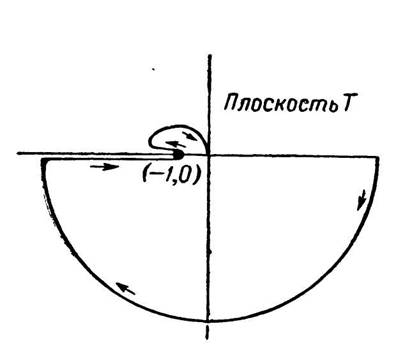
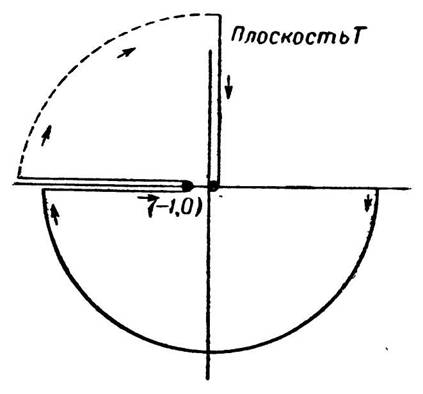
Выполнение этих условий позволяет получить максимально возможную величину обратной связи. Они приводят нас к устойчивым системам, если мы будем считать, что обе фазовые характеристики имеют бесконечно малую крутизну вблизи точки минимума и пересекают линию 180° при минимуме. Это позволяет при построении диаграмм Найквиста сделать обход непосредственно у самой критической точки, как это показано на фиг. 362 и 363, так что полное усиление по петле и значительная величина фазового сдвига вблизи частоты f_r не означают нестабильности.

Пунктирная линия дуги на второй фигуре приведена для того, чтобы показать дугу бесконечного радиуса, которая будет соответствовать точке усиления на пике и точке разрыва непрерывности фазовой характеристики на частоте f_r для кривой II на фиг. 360 и 361.

Алгебраические соотношения, к которым приводят эти условия, несколько сложны и не будут приводиться здесь. Для характеристик, определяемых соотношением (18.11), они указывают на возможность увеличения обратной связи, по сравнению с максимально возможной для случая ступенчатой характеристики среза, примерно на 4 дБ при n = 3. Степень увеличения обратной связи постепенно повышается с величиной п и достигает 8 дБ при п = 6.

Если имеет место вытекающее из соотношения (18.10) решение, соответствующее меньшему значению экстремума, то увеличение обратной связи будет на 1 или 2 дБ больше. При n>6 никакое из решений не может быть использовано, так как при больших значениях п величина фазового сдвига на частотах, лежащих выше минимума усиления, становится столь большой, что диаграмма Найквиста охватывает критическую точку при втором обходе вокруг начала координат.

Часть [1]  [2]  [3]  [4]  [5]  [6]  [7]  [8]  [9]  [10]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

Что такое интерьер знают не многие, но для настоящих профессионалов это работа. Студия Зетта составляет план интерьера под ваше желание.

Сумка мужская MONTBLANC

Это интересно

Материал, приведенный ранее, показывает, каким образом величина обратной связи, которая может быть .получена в любом усилителе, зависит от асимптотической характеристики петли обратной связи на высоких частотах.
    Поэтому представляет известный интерес установить, каким образом основные части усилителя влияют на асимптотическую характеристику и каким образом улучшение какой-либо из них сказывается на общей допустимой обратной связи.
    В предыдущем рассмотрении асимптотическая петля обратной связи считалась состоящей из двух основных частей. Одна из них включала в себя каскады канала прямого усиления, а вторая охватывала входную и выходную цепи и цепь обратной связи. Как мы уже видели, лампы определяют верхний положительный предел асимптотических значений ввиду того, что вряд ли возможно получить лучшие результаты, чем те, которые соответствуют случаю непосредственного включения цепи обратной подачи и выхода последнего каскада на вход первого каскада. Однако при заданных лампах многое зависит от того, насколько искусно проектировщик будет осуществлять цепь обратной подачи, не вводя в схему дополнительные шунтирующие емкости. Будет целесообразно продолжить здесь рассмотрение этого вопроса с тем, чтобы более детально показать, каким образом два указанных фактора влияют на величину общей допустимой обратной связи.
    Влияние, которое оказывают на полную асимптотическую характеристику усилительные каскады и элементы цепи обратной подачи, можно более отчетливо уяснить, если на фиг. 351 добавить вторую асимптоту, которая будет характеризовать усиление ламп, работающих только на собственные паразитные емкости. Это приводит нас к результатам, представленным на фиг. 364. Асимптотическая характеристика для ламп показана в виде пунктирной линии. Она пересекает ось нулевого усиления на частоте ft = Gm/2πC, где Gm и С — соответственно крутизна и емкость лампы, используемой в схеме.
    Так как величина Gm/C представляет собой так называемый ¨коэффициент качества¨, то мы можем назвать частоту ft ¨частотой коэффициента качества¨ прямого канала.
    Расстояние между двумя асимптотами обозначено величиной At. Очевидно, что эта величина равна уменьшению усиления за счет цепи возвратной подачи на частоте ft. В простейших схемах, которые, к тому же могут обеспечить наибольшую обратную связь, таких, например, как схемы, приведенные на фиг. 344 и 348, цепь обратной подачи сводится на верхних частотах к емкостному потенциометру, причем асимптотическое значение этой цепи определяется просто делением напряжения в этом потенциометре. На фиг. 364 это показано с помощью двух асимптот, имеющих равную крутизну, однако в более сложных цепях, разумеется, крутизны могут быть различны.
    Интересующее нас соотношение может быть получено, если мы выразим частоту fa, соответствующую пересечению с асимптотой, через члены ft, At и п. Это позволит заменить соотношение (18.7) следующим:
    Первый член соотношения (18.12) показывает, каким образом используемая обратная связь зависит при данной ширине полосы от Применяемых ламп. При маломощных лампах специальной конструкции частота ft может доходить до 50 или даже 100 МГц. Однако если частота f0 достаточно низка, то первый член будет иметь существенное значение даже в том случае, когда выбраны лампы с гораздо меньшей величиной ft. Второй член соотношения (18.12) показывает, насколько величина обратной связи может уменьшиться за счет остальных элементов схемы.
    Если детали в усилителе размещены рационально и все остальные конструктивные требования выполнены удачно, то этот член может давать лишь 10—15 дБ. При использовании современных ламп, второй член соответствует такому порядку величин, при которых усилитель должен иметь достаточно большую обратную связь при ширине рабочей полосы в несколько мегагерц. С другой стороны, если в отношении входной и выходной цепей, а также в отношении цепи обратной связи установлены очень жесткие требования или если рабочая полоса настолько узка, что соответствующая величина обратной связи может быть получена даже при отсутствии тщательно выполненной конструкции, то второй член может иметь существенно большее значение.
    Оптимальное число каскадов в усилителе с обратной связью
    В соотношение (18.12), помимо величин ft и Аt входит также асимптотическая крутизна п. Так как лампы не вызывают завала асимптотической характеристики на частоте f = ft, то мы можем варьировать величину п путем изменения числа ламп схемы, не воздействуя при этом на значение At. Это дает возможность подсчитать оптимальное число ламп, которое должно быть применено для каждого данного случая, с тем, чтобы получить максимально возможную величину обратной связи.
    Если At мало, то первый член соотношения (18.12) будет иметь преобладающее значение, и очевидно, что здесь желательно иметь малое число каскадов. В качестве предельного значения можно принять n = 2, так как в случае лишь одного каскада степень обратной связи ограничивается величиной усиления по прямому каналу, что не было принято во внимание в настоящем анализе. С другой стороны, ввиду того, что второй член изменяется с величиной п более быстро, чем первый, оптимальное число каскадов будет возрастать, если At возрастет. В общем случае оно определяется соотношением
    или, другими словами, оптимальное число каскадов равно выраженной в неперах величине завала асимптотической характеристики.
    Результат, который получится, если мы выберем число п больше или меньше оптимального, можно установить, полагая n = λ(At /8,68). Это позволяет переписать (18.12) в виде
    Очевидно, что первый член характеризует обратную связь, получающуюся при оптимальном числе каскадов, а второй член — то уменьшение обратной связи, которое вызвано использованием числа каскадов, отличного от оптимального. График для второго члена изображен на фиг. 365. Из него видно, что проигрыш получается сравнительно незначительным, если мы выбираем число каскадов в пределах от 0,5 до 2 от оптимального значения, однако при более существенном отклонении ухудшение будет значительно более заметным.
    Далее...