Это интересно

Минуло только три года с момента появления моей статьи «Transformer Coupled WE-300B, Single-Ended Amp» (GA 1/94), которая, я полагаю, стала первой по данному типу усилителя в этом журнале. Как я был поражен, увидев череду однотактников на зимней выставке WCES'96 в Лас Вегасе, где прежде героями ходили транзисторные монстры. Мне трудно было поверить, что американские аудиофилы способны воспринять DHT-SE* ничтожной мощности даже после того, как издатель Glass Audio Эдвард Делл (Ed. Dell) подбил меня написать что-либо об audio в Японии и особенно об однотактниках.
    Мне известно, что Jean Hiraga**, живший в Японии одно время, в своих статьях защищал японский audiocraib — DHT-SE и рупорные громкоговорители. Сейчас он работает во Франции и в Европе его деятельность довольно популярна. Но в Америке? Стране гигантских мощностей и гигантского всего остального. Я был крайне скептично настроен. Однако, реакция читателей на мои письма в GA заставила внонь обратиться к теме, что именуется мистическим японским аудиосообщестзом. Сама выставка WCES'96 и многочисленные ревю о DHT-SE в журналах убедили меня в том, что тема однотактников воспринята в Америке с энтузиазмом, запредельным для моего понимания. Только теперь я исполнен вдохновением большим, чем когда-либо, писать об однотактниках.
    Улучшений 300В SE усилитель
    Я спроектировал и построил усилитель на 300В с межкаскадным трансформатором в конце 70-х и полагал, что поставил точку в моих бесконечных играх с 300В. Однако, я ошибался. Выходит, что для улучшений еще остался запас. На рис. 1 дана схема моей новой улучшенной версии, включая все изменения, внесенные мной в первоначальную, опубликованную в GA 1/94. Наиболее значительным изменением было удаление конденсатора между первым каскадом и драйвером. Возможность прямой связи в предыдущих каскадах оправдывает значительную выгоду от применения межкаскадного трансформатора. Из-за того, что резистивное сопротивление первички IT (Interstage Transformer) мало, мы без усилий получаем высокое напряжение питания на аноде драйвера. Его хватает, чтобы и на катоде оно было столь высоким, чтоб управляющую сетку непосредственно соединить с выходом каскада усиления напряжения. При этом еще остается достаточная разница между анодом и катодом, чтобы драйверу работать в подходящем режиме.
    Второе улучшение: схема SRPP входного каскада, главным образом отвечающего за усиление напряжения. Это позволило исключить большое сопротивление в аноде, потенциальный источник ухудшения звука.
    Теперь я могу честно признаться, что не знаю, почему схема с межкаскадным трансом звучит лучше, равно как не знаю, почему сопротивление порядка нескольких десятков кОм на пути сигнала способно ухудшать звучание. Ведь восточная культура тем и отличается от западной, что мы менее расположены добиваться ответа на «почему это так работает», чем найти, что это вот работает, а вот это — нет. Другими словами, восточная культура более склонна к эмпирике, нежели к аналитическому изучению.
    Хорошим примером здесь является китайская медицина, которая работает, но при этом не сходится с западной научной аналитической медициной. Мы не восприняли бы так однотактники, если б необходимо было перед тем «научно» объяснить их феномен. Однако, я не хочу, чтобы это понималось как то, что мы не желаем знать, почему так происходит. В связи с этим я глубоко признателен Reid'y Welch'y за попытку объяснить, почему межкаскадный трансформатор так работает (см. статью в GA «Driving the 300B» в 1/96). Это и есть прекрасный пример взаимосвязи двух культур.
    Межкаскадник можно и подешевле
    Мне известно, что многих любителей смущает запредельная цена межкаскадного транса Tango NC-20, который я использую. С этой целью я публикую информацию об альтернативных изделиях японского происхождения.
    Таким можно считать Tango NC-16. Если вы соедините параллельно обе первичные обмотки, он будет держать ток 30 mА и импеданс первичной обмотки 2,6 кОм — вполне нормальный для 6F6 в триодном включении. Вы можете также включить параллельно вторичные обмотки, при этом получить трансформацию 1:2 и расширить диапазон. Можно их соединить последовательно и добиться увеличения напряжения в 4 раза, но при этом диапазон станет несколько уже. Стоимость NC-16 вдвое меньше цены NC-20.
    Вы также можете использовать Tamura A-342. Для всех межкаскадных трансов Tamura характерно одно слабое место — суженный частотный диапазон, обычно от 30-50 Гц до 15 кГц,хотя качество их в этом диапазоне нареканий не вызывает. Другой их недостаток в том, что они довольно габаритны. Зато они выигрывают по цене. Помните, однако, что качество выходного трансформатора вместе с межкаскадным столь же важно, как и качество ламп. Потратьте на них столько, сколько сможете себе позволить, и лишь потом думайте об экзотических резисторах с конденсаторами. Их вы можете заменить позже, когда будут деньги.
    Уменьшение искажений находится в противоречии с мощностью на аноде.
    Существует два пути уменьшения гармонических искажений в триодных однотактниках. Один из них — увеличение нагрузки в анодной цепи. Как видно из табл. 1, при тех же значениях Ер (напряжение на аноде) и Iр (анодный ток без сигнала) и, следовательно, при той же мощности на аноде, мы получим меньшие искажения при увеличении сопротивления нагрузки R(, правда ценой максимально возможной выходной мощности. То есть, полезная мощность в нагрузке снизится.
    Положим, к примеру, рабочие условия для 300В: Ep=350V, Ip=60mA. Тогда мощность на аноде равна 21 Вт. При RL = 2 кОм в выходном сигнале содержится -21 дБ (около 10%) второй гармоники и -30 дБ (около 3 %) третьей гармоники при максимально возможной мощности 10,2 Вт, когда заметно клиппирование входного сигнала или отсечка выходного (либо оба условия выполняются одновременно). Если мы возьмем нагрузку RL = 3 кОм, то вторая гармоника будет равна —26 дБ (5 %), третья равна - 38 дБ (1,3 %), то есть вполовину меньше, чем было с нагрузкой в 2 кОм. Но мощность теперь уменьшилась до 8,3 Вт. Когда же возьмем RL =- 4 кОм, гармоники станут еще ниже: вторая -30 дБ (около 3 %), третья -44 дБ (около 0,6 %), а мощность упадет до 7 Вт. Так как кривые искажений для каждой RL пойдут параллельно друг другу в координатах выходной мощности,до определенного предела, мь могли бы ожидать дальнейшего снижения искажений при увеличении RL (в области мощностей ниже предельных). Но опять таки ценой падения максимально возможной мощности, которая соотносится с мощностью рассеяния на аноде. (Здесь принят термин эффективность анода, представляющий отношение выходной мощности к мощности, рассеяной на аноде — примечание Ред.).
    При 2 кОм мы получим эффективность анода 49 %, при 3 кОм — 40 %, и при 4 кОм 33 %. То есть, имеем своеобразный обмен полезной мощности (падающей) на затраты энергии (растущие), нужно лишь определиться с подходящей нагрузкой для каждой конкретной цели.
    Далее...

Измерение характеристик выходного трансформатора

ЧАСТЬ 1

Menno J. Van der Veen, Glass Audio 5/97

В номере 1/95 Рик Берглунд опубликовал интересную статью об измерениях OPT (output transformer)1. Как разработчик широкополосных выходных тороидальных трансформаторов (компания Plitron, серия PAT) ^2,3, я был рад появлению столь весомого материала, где указаны инструменты оценки. Я испытал его методы и нахожу, что они оправданы и надежны. В его статье содержатся также важные положения, которые, я полагаю, требуют особого внимания:

«Трансформатор с наименьшим значением тока и наиболее прямой линией зависимости тока от поданного напряжения, даст наименьшие искажения по басу... Трансформатор с высоким значением индуктивности первички не обязательно даст минимум искажений по отношению к трансформатору с меньшей индуктивностью... Высокоиндуктивный трансформатор может обладать весьма нелинейной зависимостью тока от напряжения.»

Что все это означает? Что происходит в выходном трансе? Как и почему он искажает поданный на него сигнал? Как можно избежать этих искажений? Какой процент искажений плох? С этими вопросами я и приступил к измерению индуктивности вторичной обмотки.

Измерение индуктивности вторичной обмотки

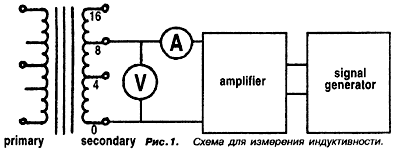
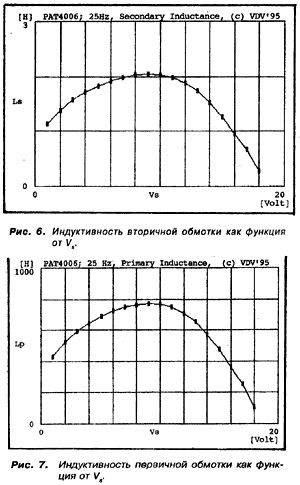
На рис. 1 (из статьи Берглунда) представлена схема измерений. Напряжение частотой 20 Гц или 25 Гц подано на выводы 0-8 Ом. Первичная обмотка остается разомкнутой, поэтому, соблюдайте осторожность, так как напряжение на ней может оказаться очень высоким. Результаты измерений Берлунда сведены в табл. 1; я же привел эти значения в виде графиков на рис. 2 и добавил измерения на тороидальном РАТ4006. Правда частота была не 20 Гц, а 25 Гц, с тем чтобы уравновесить условие измерений, так как вторичка у Т4006 рассчитана на 5 Ом против 8 Ом в образцах Берглунда.

Графики имеют ощутимые различия и причина тому в разных конструкциях и применяемых материалах. Минимальные значения тока указывают на максимальную индуктивность. Из-за того, что точек измерения недостаточно, кривые представлены довольно грубой аппроксимацией, поэтому я увеличил число измеряемых точек и представил РАТ4006 на рис. 3. Из графика видно, что поведение Is/ Vs (индекс S — secondary, относится к вторичной обмотке. Прим. переводчика) подобно прямой линии в очень широком диапазоне. Очевидно это удовлетворяет требованию, выведенному Берглундом в статье. Однако, линейность может быть выражена языком аналитическим, то есть, более детально: при абсолютной линейности, отношение Vs/ Is в любой точке , должно быть величиной постоянной (рис. 4). При том, что индуктивное сопротивление со стороны вторички велико, очевидно явное отклонение от прямой линии. В соответствии с этим, в определение Берглунда о линейных свойствах трансформатора я внес бы дополнения: линейность характеристики 4 (VJ может быть рассчитана как импеданс вторички Zs = Vs/Is(Vs).

Вычисление индуктивности

Что же представляет собой отклонение от прямой линии значение индуктивного импеданса, и чем это вызвано? Чтобы ответить на этот вопрос , мы должны исследовать поведение материала сердечника. Из рис. 4 явно следует, что девиации вызваны эффектами, происходящими в железе и ничем иным. Чтобы нащупать их, я изобразил эквивалентную схему трансформатора для низких частот со стороны вторичной обмотки (рис. 5). Ris — активное сопротивление меди вторички. Потери в железе на гистерезис и вихревые токи представлены Rc Третий элемент в схеме — индуктивность вторичной обмотки. Чтобы формализовать реакцию этой цепочки, я намеренно исключил влияние потерь в железе, которые заметно проявляются только при насыщениии . На средних уровнях мощности соотношение Vs/Is от частоты выглядит так:

Vs/Is = R_is + i + 2pfL_S   , i=Ц-l   (1)

Удалив мнимую часть в формуле, затем можно вычислить Ls:

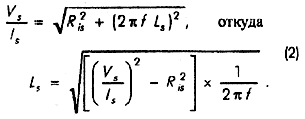
Величина активного сопротивления измеряется просто, тогда можно вычислить значение Zs для любой частоты (естественно Vs/Is должны быть измерены по схеме на рис. 1).Результаты представлены графиком на рис. 6 , тогда как на рис. 7 приведен график индуктивности со стороны первичной обмотки, вычисленной по известной формуле: Lp=Ls х (Np\Ns)². Np и Ns означают число витков в первичной и вторичной обмотках соответственно.

Из графика видно (равно как из расчетных значений), что величина 4 непостоянна. Так как Ris очень мало (0,18 Ом), кривая зависимости 4 от напряжения на вторичке будет повторять ход кривой Vs/Is . Вот теперь мы с полным правом можем задаться вопросом более предметным: что же заставляет изменяться индуктивность вторички?

Исследование сердечника

Когда ток проходит по виткам катушки на сердечнике, он образует магнитное поле и частицы (или группы частиц, называемые площадками Вейсса, в просторечии — доменами) начинают разворачиваться и сдвигаться (эффект магнитострикции). И чем легче они разворачиваются (затрачивается меньшая энергия), тем выше плотность магнитного потока в сердечнике (индукция). Тем самым магнитное поле сильнее влияет на разворот всех доменов в одном направлении. Их подвижность и соотношение ориентированных площадок к развернутым произвольно выражается относительной магнитной проницаемостью m_r . Чем выше это значение, тем сильнее реагирует сердечник на поле, созданное вторичной обмоткой.

Все изменения в ориентации доменов порождают сложные частные магнитные взаимодействия площадок между собой, приводящие к специфическому шуму на концах обмотки. Оно имеет название «эффект Баркгаузена» и его величина зависит от качества используемого железа. Важным критерием при выборе материала сердечника является малость эффекта Баркгаузена. В результате m_r, влияет на величину и нелинейность Ls:

L_S = (m₀ґ m_r ґ N_s² ґ l _m ) / A    (3)

где m₀ = 4m х 10^-7, N_s — число витков вторички, А — площадь сечения магнитного сердечника, lm — длина средней магнитной линии в сердечнике. Последние имеют размерность метра.

Для формулы 3, в применении к выходному трансформатору, все составляющие постоянны, кроме m_r . Так как m_r оценивает подвижность магнитных частиц в материале сердечника, то открытие самой подвижности (факт научный) и может служить дальнейшим объяснением нелинейного поведения m_r . При насыщении сердечника, все домены развернуты Е; одном направлении и не могут развернуться куда-либо, для занятия более «лучшего» положения. Соответственно магнитная проницаемость m_r почти равна нулю. При очень малых уровнях намагничивания, взаимодействие полей внешних и полей собственно доменов таково, что возникает равновесие, и это позволяет удерживать домены в первичном состоянии. Опять mr невелико (начальная проницаемость). Где-то между этими двумя крайними точками способность к движению у доменов оптимальна, тогда и m_r достигает максимального значения. Это находит отражение на рис. 6 и рис. 7.

Представьте теперь, что указанная подвижность является главной причиной того, почему энергия (звуковая) из выходных ламп может быть трансформирована в энергию излучения громкоговорителя. После этого станет понятно — трансформатор очень «непростое» устройство и поведение его далеко от линейного.

Сравните сложность процессов (их нелинейность) в трансе с работой лампы, чей анодный ток подчиняется четким и простым правилам, или взять транзистор, где существуют чисто логарифмические соотношения. Они просты и очевидны в сравнении с OPT (outpirt transformer). Тогда отчего же не выбросить его вовсе? Да оттого, что на самом деле он не так плох как кажется и звучит просто здорово. Я попытаюсь объяснить это, рассмотрев присущие ему нелинейности.

Вычисление искажений ОРТ

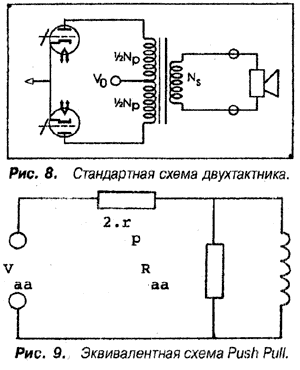
В начале возьмем для рассмотрения двухтактную схему, стандартно изображенную на рис.8. Каждая лампа в плече имеет эффективное сопротивление (внутреннее) r_P. Вторичка ОРТ подключена к громкоговорителю с импедансом Z_L. Положим, что сопротивление нагрузки независимо от частоты и постоянно. На стороне первичной обмотки оно приобретает величину R_aa, равную почти 2 кОм для РАТ4006. На рис.9 показан низкочастотный эквивалент этой цепи со стороны первичной обмотки.

Выходные лампы здесь заменены источником напряжения с последовательно включенным резистором 2 х r_P (В этой дискуссии я опускаю активные сопротивления проводов обеих обмоток, так как влияние их на нелинейность минимально). Теперь наш усилитель начал работать и между анодами на сопротивлении R_aa появилось переменное напряжение, а значит потек переменный ток по цепи на рис.9.

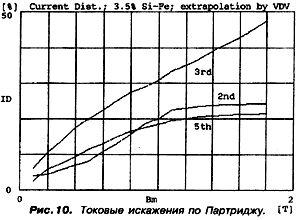
Ток, проходящий через индуктивность порождает магнитное поле, которое в свою очередь создает напряжение на концах вторичной обмотки ОРТ. Но если L_р (в силу уже известных нам причин) непостоянно, то и ток испытывает искажения. А вот напряжение на выходе, будет ли оно иметь те же искажения? Природа искажений была исследована Dr. Partridge'M . На рис. 10 показаны результаты его измерений на сердечнике с 3,5 % содержанием кремния. На ординате отложены искажения по току в процентах, по абсциссе — ппотность магнитного потока, то есть индукция в теслах (Тл). ( Плотность магнитного потока есть число магнитных силоных линий, проходящих по сечению с площадью А.) Кривые на графике означают соответственно 2-ю, 3-ю, 5-ю гармоники соответственно.

Для оценки искажающих свойств ОРТ в общем виде, я предположил, что образцы трансформаторов на рис. 2 (характеристики тока) имеют тот же материал сердечника, что и на рис. 10 (характеристики токовых искажений). Чтобы получить B_max (амплитудное значение) , необходимо воспользоваться значением Vs (напряжение на вторичной обмотке) по формуле 4:

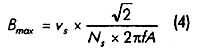
Чтобы вычислить искажения по напряжению, Партридж предложил следующую формулу:

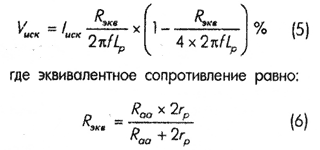
Теперь мы имеем полную необходимую информацию для оценки искажений по напряжению на любой частоте и выходном напряжении, в предположении, что материал сердечника тот же, что указан на рис. 10.

Влияние самих ламп на искажения

Я использовал вышеуказанную методику для вычисления искажений трансформатора РАТ4006 при работе с четырьмя 6550WA (Sovtek); в каждом плече двухтактника по две лампы параллельно. В пентодном включении эффективное сопротивление (суммарное, т. е. 2r_P ) равно 7,5 кОм, в ультралинейном (40 % отвод от первички) — около 2 кОм. При включении триодами, сопротивление равно 750 Ом^*. Подсчитанные искажения отражены на рис. 11, 12 и 13 соответственно.

Отсюда вытекает общее правило: чем меньше внутреннее сопротивление источника (в данном случае лампы), тем меньше искажения. В своей статье Hodgson использует этот вывод для объяснения того, почему триоды звучат лучше, чем пентоды. Взяв предложенные Партриждем выкладки за основу, я нашел, что искажения ОРТ при работе с триодами действительно ниже, чем с пентодами. Так что я согласен с общими выводами Т. Hodgson'a.

На рис. 14 отражена ситуация, когда частота сигнала равна 50 Гц вместо прежней 25 Гц, лампы в ультралинейном включении. Искажения в этом случае много меньше, чем при 25 Гц. Еще одно общее правило: с повышением частоты, искажения в трансформаторе падают. В дальнейшем я покажу важность этого эффекта в объяснении специфического характера звучания ламповых усилителей.

Из рис. 15 становится понятен следующий вывод: с уменьшением индуктивности L_P искажения резко повышаются. В этом случае я предположил, что ток в РАТ40С6 в десять раз больше против того, что на рис. 2, что является результатом десятикратного уменьшения индуктивности. Это вполне объясняет, насколько важна величина L_P для получения неискаженного звука на низких частотах.

Насколько же плоха нелинейность?

Во всех графиках искажений можно отметить явную однородность. По ним не разглядеть изменений m_r, равно как Lp и Ls не выглядят определяющим фактором. Кое-как вариации Lp и Ls проявляются в формуле (5), хотя искажения выходного напряжения заметно меньше токовых. Только на пороге насыщения , где указанные индуктивности резко падают, искажения начинают стремительно расти. Довольно неожиданный результат; как же все это понимать? Математически можно без особого труда вывести, что ниже точки насыщения, искажения напряжения малы и почти не зависят от колебаний m_r, когда выполняется условие:

2p fL_P>> R _экв   (7)

Таким образом, большая индуктивность первички выполняет роль абсолютно существенную в удержании искажений на низком уровне, так как только ее величина влияет на удовлетворение неравенства (7). В момент равенства левой и правой части, искажения приобретают большую зависимость от m_r. Примером тому служит график на рис. 15, где L_P взята в 10 раз меньше. Так что, ОРТ с большой индуктивностью (и следовательно малыми токами, измеренными по методу Берглунда), является условием получения малых искажений.

Порою, однако, требуется спроектировать трансформатор с невысокой индуктивностью первички. Такое случается с однотактными трансформаторами, когда необходимо создать баланс между насыщением и по переменному, и по постоянному току. А это приводит к получению индуктивности гораздо меньшей, чем в двухтактнике. Условие (7) не может быть выполнено, остается лишь обеспечить постоянство m_r. Мы можем это реализовать двумя путями, выбором специального материала сердечника и точной настройкой ширины зазора.

Каков же окончательный результат моих поисков? Я готов добавить условие (7) к методам тестирования Берглунда. Оно является важным при оценке насколько плох или хорош ОРТ для определенных применений, поскольку по спецификации на трансформатор этих выводов сделать нельзя. Мы должны максимально точно сформулировать требования к ОРТ и выглядят они следующим образом: R _экв и нижняя частота работы должны быть сравнимы с индуктивностью первичной обмотки. Только после этого можно заключить, насколько оптимально применение данного трансформатора.

Часть [1]  [2]

Вестник А.Р.А. №4

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

Предлагаем абонентское юридическое обслуживание lawtax.ru

Производство бумажных пакетов

Паяльное оборудование HAKKO, PACE, OKi.

Электронные компоненты Продажа электронных компонентов. Интернет магазин.

Это интересно

У меня накопилась огромная информация с объяснением специфического характера звучания ламповых усилителей. Я сосредоточился главным образом на звучании баса, так как именно здесь искажения выходного трансформатора доминируют над всеми искажениями схемы. Формула (7) дает значение частоты, ниже которой искажения по напряжению становятся угрожающими.
    На выходе усилителя, чьи искажения ниже 40 Гц резко растут, мы намеряем хвост из гармоник: 80 Гц — вторая, 120 Гц — третья и так далее. Когда мы станем слушать этот сигнал, то услышим не продукты искажений, а сильный, богатый бас.
    Этот тест выявляет удивительную способность нашего слуха конвертировать набор искажений в основную составляющую. Нам слышится 40 Гц и, благодаря присутствию гармоник, этот тон воспринимается громче и интенсивнее. Также был проведен опыт, когда на выходе усилителя основной тон удалялся и оставались только гармоники6. В этом случае казалось, что мы ясно слышим этот тон, гармоники словно воссоздавали его.
    Указанный эффект имеет место только в басовой области, когда середина и высокие остаются неискаженными. Таким образом эти искажения проявляются не как хрипы, но как вполне приемлемое для уха звучание, ничуть не раздражающее.
    Но что же произойдет, когда мы используем выходной трансформатор с очень большой индуктивностью? Может быть, это удивит вас, но бас будет звучать мягче. Искажений не возникает, вы слышите только чистый тон. Это обнаружилось при работе с PAT 4006.
    Во время теста я заметил, что звучание тороидального транса несколько мягче, чем звук трансформатора на Ш-железе с невысокой индуктивностью (всего ЗО Гн). Частотная характеристика, благодаря громадной индуктивности тора, протягивается вниз гораздо дальше, чем у обычного (Ш-пластины). Вроде бы бас должен восприниматься громче, но это не так. Соображения, приведенные выше, как раз объясняют этот факт, а я оставляю вам судить, насколько желаемы или нет искажения в басу.
    Высказанная теория проясняет, отчего же выходные трансформаторы в разных приложениях могут звучать различно. Она же объясняет, отчего в гитарных усилителях они играют решающую роль в создании специфического тонального баланса и почему трансформаторы с солидными размерами не используются там. Эта модель способна объяснить, почему в качественных hi-end аппаратах мы встречаем трансформаторы огромных размеров: они таковы, чтобы искажения на низких частотах были низки насколько возможно. В этом свете тороидальные ОТ как раз следуют выдвинутой теории.
    В предыдущем обсуждении и взаимодействии акустики и усилителя я исходил из того, что последний работал без ОС. Я также полагал, что в нашем распоряжении нет громкоговорителя с постоянным импедансом, не зависящим, от частоты. Представьте теперь идеализированный усилитель с абсолютно линейной частотной характеристикой, линейностью передачи без искажений и совершенными временными параметрами.
    Такой вот «идеальный» прибор, при подключении его к нормальной акустике с гуляющим импедансом, может вызвать специфические эффекты. Нет, я не имею в виду, что усилитель начнет возбуждаться. Я говорю о совершенно другом эффекте, ранее изученном и до ныне остающимся очень важным, рис. 16 представляет эквивалентную схему усилителя и подключенную к ней нагрузку ZL.
    Благодаря совершенной частотной характеристике и отсутствию общей обратной связи, выходной импеданс такого усилителя будет частотнонезависим. Положим, что усиление равно А при входном напряжении Vin . Тогда выходное напряжение Vout на клеммах акустики будет определено формулой (9):
    В этой формуле коэффициент демпфирования представляет собой отношение импеданса нагрузки к выходному сопротивлению усилителя DF = ZL/Zout. паспорте на усилитель обычно указан импеданс нагрузки в 8 Ом, так что при выходном сопротивлении усилителя в 2 Ом, DF= 4.
    Однако в реальной ситуации из-за того, что импеданс громкоговорителя изменяется с частотой, действительный коэффициент демпфирования постоянным не будет. Следовательно, как показывает формула (9), напряжение на входе динамика будет также изменяться с частотой.
    Но, большинство громкоговорителей спроектированы на то, чтобы напряжение на зажимах поддерживалось постоянным во всем диапазоне частот и, таким образом, давление на оси (SPL — Sound Pressure Level) оставалось бы постоянным. С ламповыми усилителями с низким коэффициентом демпфирования дело обстоит иначе.
    Чтобы исследовать этот факт, я построил усилитель с регулируемым DFM подключил его к головке электродинамического типа, попросту — к обычному дифузорному излучателю с подвижной звуковой катушкой. У меня была возможность выставлять коэффициент демпфирования в 100, 8, 4, 2 и 1 (по отношению к 8-омной нагрузке). Измерения давления выполнялись калиброванным микрофоном в хорошо заглушенном помещении. Характеристика громкоговорителя при DF = 100 была взята за эталон, так что остальные графики дают лишь степень отклонения от этой характеристики, не являясь при этом собственной частотной характеристикой динамика. Результаты на рис. 17.
    Результаты оказались поразительными. Чем меньше коэффициент демпфирования, тем большее отклонение характеристики от эталонной. Ламповые усилители, особенно без ОС, имеют весьма малый DF и таким образом большой завал высоких частот. Я повторил эксперимент с разными динамиками и характер графиков подтверждал общее правило.
    Однако, прослушивание этих громкоговорителей не выявило большой разницы при изменении DF от 1 до 100. Почему же я не заметил субъективных изменений частотной характеристики? Не я один, поскольку ламповые усилители с ОС или без нее широко распространены в мире, и я не слышал нареканий в их сторону. Объясняю это тем фактом, что ухо человеческое быстро адаптируется к изменениям частотной характеристики, если они не происходят очень быстро. Но пойдем дальше.
    Далее...