Это интересно

Ионный ток. Одной из причин возникновения обратного тока сетки является ионизация остаточного газа, которая всегда имеет место при высоких ускоряющих напряжениях анода. Положительные ионы, образующиеся в междуэлектродном пространстве, устремляются в сторону отрицательно заряженных электродов, в том числе на сетку. На поверхности сетки ионы рекомбинируют с электронами, превращаясь в нейтральные атомы, диффундирующие вновь в разрядное пространство. Взамен электронов, потерянных сеткой вследствие ре­комбинации, в нее из внешней цепи поступают новые электроны, воз­никает ток, направленный навстречу току сетки, обусловленному на­чальными скоростями электронов, эмиттированных катодом. Его на­зывают ионным током сетки.
    Ионный ток сетки определяется числом возникающих в лампе по­ложительных ионов, которое зависит от плотности остаточного газа, величины анодного тока, конструкции лампы и свойств наполняющего ее газа:
    I_ci = G_vI_а(9.24)
    Величину G_v называют коэффициентом вакуума. В хорошо откачанных лампах она имеет порядок 10^-5 - 10^-6.
    Термоток. При большой мощности накала катода, близком распо­ложении сетки от катода, перегреве сетки тепловым излучением анода возникает термоток сетки. Для уменьшения термотока стремятся сни­зить температуру сетки с помощью массивных, хорошо отводящих теп­ло траверс и радиаторов, а также путем улучшения теплоизлучения. Иногда для уменьшения термотока сетку покрывают золотом. В этом случае барий, испаряющийся с катода и осаждающийся на поверх­ности сетки, быстро диффундирует в глубь покрытия, не вызывая сни­жения работы выхода сетки. Золото имеет значительную работу вы­хода (4,99 эВ), поэтому термоток сетки получается небольшим.
    Ток утечки. Несовершенство изоляции сетки, в первую очередь относительно анода, вызывает появление еще одной составляющей об­ратного тока сетки — тока утечки. Он зависит от сопротивления изо­ляции сетки и разности потенциалов сетка — анод:
    В исправных лампах сопротивление изоляции R_из достигает 200 МОм и более, но со временем оно может снизиться вследствие напыления на изоляцию активирующих веществ с катода, газопоглотителя и ме­талла электродов. В этом случае ток утечки может стать недопустимо большим.
    Характеристики триода при положительных напряжениях сетки
    При положительных напряжениях сетки катодный ток триода рас­пределяется между сеткой и анодом, при этом
    I_к = I_а + I_с    (9.26)
    Закономерности токораспределения при положительных напряжениях сетки можно уяснить из передаточных (анодно-сеточных) харак­теристик триода (рис. 9.11). При повышении положительного сеточного напряжения вначале наблюдается увеличение анодного тока, но затем при U_с ≈ U_а анодный ток замедляет рост и, достигнув максимума, начинает уменьшаться; сеточный ток продолжает возрастать.
    Зависимость сеточного тока от анодного напряжения хорошо вид­на на сеточно-анодных характеристиках триода (рис. 9.12). Сеточный ток имеет максимальное значение при нулевом напряжении анода, а с увеличением анодного напряжения он падает вначале относительно быстро, а затем при U_а>U_с — более медленно. Анодный ток при увеличении анодного напряжения от нуля резко возрастает, а при U_а>U_с рост его становится более медленным.
    Анализ рассмотренных характеристик приводит к выводу о том, что в триоде при положительном напряжении сетки существуют два режима токораспределения, подчиняющихся различным закономерно­стям: один {режим перехвата электронов) — при напряжениях сетки, меньших анодного, когда с превышением сеточного напряжения воз­растают оба тока — анодный и сеточный; другой (режим возврата электронов) — при напряжениях сетки, больших анодного, когда с повышением сеточного напряжения возрастает только ток сетки, а анодный ток уменьшается...
    Далее...

ЧАСТЬ 4

ДИФФЕРЕНЦИАЛЬНЫЕ ПАРАМЕТРЫ ТРИОДА

Дифференциальными параметрами называют величины, связываю­щие малые приращения токов и напряжений в электронном приборе. Критерием малости приращений является наличие линейной зависи­мости между ними, иначе говоря, независимость параметров от вели­чины приращений.

Дифференциальные параметры называют статическими, если их определяют в статическом режиме (через разности соответствующих величин для двух близких статических режимов).

Рассмотрим случай, когда напряжение сетки отрицательно, следо­вательно, сеточный ток практически равен нулю. Анодный ток при постоянном напряжении накала является функцией двух переменных — напряжения сетки и напряжения анода:

I_а=f(U_с; U_а)(9.29)

Запишем выражение для полного дифференциала:

Частные производные в этом выражении определяют приращения тока при изменении напряжений электродов и поэтому могут быть взяты в качестве дифференциальных параметров триода.

Статическими параметрами триода являются: S=dI_а / dU_с — крутизна;  G_ак=dI_а / dU_a — выходная проводимость. Использовав эти обозначения, получим

dI_а= SdU_с + G_акdU_a(9.31)

Рассматривая приращения независимых переменных dU_a и dU_с как малые гармонические переменные напряжения с амплитудами U_ma и U_mc, найдем, что в диапазоне низких частот, когда не сказывается влияние междуэлектродных емкостей, индуктивностей вводов и инерции электронов, приращение dI_а будет представлять собой также гармоническое колебание с амплитудой I_ma:

I_ma = SU_mc + G_акU_ma(9.32)

Крутизна

Как и в полевых транзисторах, крутизна S = ∂I_а / ∂U_с характеризует управляющее действие, в данном случае сетки, и численно рав­на величине изменения анодного тока, приходящейся на 1 В измене­ния сеточного напряжения при постоянном напряжении анода. Вы­ражается крутизна в миллиамперах на вольт или в микроамперах на вольт. Название этого параметра обусловлено тем, что он показы­вает, насколько круто поднимается передаточная характеристика лампы.

Зависимость крутизны от конструкции лампы можно найти с по­мощью закона степени трех вторых (9.17), если ограничиваться слу­чаем отрицательного напряжения сетки. Взяв производную от тока по напряжению сетки, получим

или

Формула показывает, что крутизна возрастает при увеличении размеров электродов и уменьшении расстояния сетка — катод. Так как размеры электродов обычно определяются мощностью лампы, то основным способом увеличения крутизны является приближение сетки к катоду. Обычно крутизна у маломощных ламп имеет величину порядка 5—10 мА/В.

В некоторых современных лампах расстояние сетка — катод составляет всего 10—15 мкм и крутизна может доходить до 50 мА/В. Даль­нейшее уменьшение этого расстояния связано с большими технологи­ческими трудностями.

Из соотношения (9.33), а также из характеристик рис. 9.8 вытекает, что с повышением анодного напряжения и снижением отрицательного напряжения сетки крутизна характеристики возрастает. При переходе в область положительных напряжений сетки рост анодного тока замедляется вследствие появления сеточного тока (см. рис. 9.11), при этом крутизна начинает уменьшаться.

Крутизна характеристики зависит и от накала катода. Поверх­ность реального катода неоднородна, на ней существуют участки с различной работой выхода и, следовательно, с различной плотностью эмиссионного тока. При снижении температуры катода уменьшаются размеры активных участков, дающих достаточную эмиссию, и эффектив­ная поверхность катода сокращается. Это приводит в соответствии с выражением (9.33) к уменьшению крутизны. В лампах с прямонакальными катодами уменьшение эффективной поверхности катода при сни­жении его температуры связано также с возрастанием длины охлаж­денных концов.

Зависимость крутизны характеристики от напряжения накала может обусловливаться сопротивлением катодного покрытия r_к, которое включено одновременно в сеточную и анодную цепи, что приводит к уменьшению крутизны:

При снижении температуры катода сопротивление катодного по­крытия возрастает и крутизна уменьшается. В лампах, имеющих очень малое расстояние сетка—катод, зависимость крутизны от на­пряжения накала может быть вызвана также изменением местоположе­ния и высоты минимума потенциала при изменении температуры ка­тода.

Выходная проводимость

Из закона степени трех вторых (9.20) получаем, что при U_с≤0 вы­ходная проводимость триода

Сравнивая с выражением (9.33), видим, что при U_с≤0

G_ак = SD.(9.36)

Помимо выходной проводимости лампы часто используют обратную ей величину — внутреннее сопротивление:

R_i = 1/G_ак(9.37)

Из формулы (9.36) следует, что внутреннее сопротивление лампы тем меньше, чем больше ее крутизна и проницаемость. Обычно внут­реннее сопротивление трехэлектродных ламп составляет 1—100 кОм.

Из соотношения (9.35) вытекает зависимость внутреннего сопро­тивления лампы от режима. Поскольку проницаемость сетки опреде­ляется отношением междуэлектродных емкостей и в первом прибли­жении не зависит от напряжений анода и сетки, изменение внутрен­него сопротивления лампы при изменении режима обратно пропорцио­нально изменению крутизны: R_i=const/S.

Коэффициент усиления

Для сравнительной оценки воздействия сеточного и анодного на­пряжений на анодный ток вводят еще один параметр — коэффициент усиления лампы μ, равный отношению приращений напряжений анода dU_a и сетки dU_c, вызывающих одинаковое приращение анодного тока. Коэффициент усиления показывает, во сколько раз приращение напряжения анода больше, чем равноценное по воздействию на анодный ток приращение напряжения сетки.

При определении коэффициента усиления μ приращения напряже­ний анода и сетки обычно берут с противоположным знаком, так, что­бы результирующее приращение анодного тока было равно нулю. Тогда

При отрицательном напряжении сетки коэффициент усиления свя­зан с проницаемостью D простой зависимостью, которую нетрудно найти из закона степени трех вторых (9.20):

I_а = g_т(U_с+DU_а)^3/2

Приращение анодного тока при изменении анодного и сеточного напряжений

Если приращения dU_с и dU_а имеют такую величину, что dI_а=0, то

Отсюда в соответствии с выражением (9.38) находим, что при U_с≤0

D = 1 / μ(9.39)

Так как, по определению, D = C_ак/C_ск, то μ = C_ск/C_ак, следовательно, коэффициент усиления лампы тем выше, чем меньше емкость анод—катод, т. е. чем гуще сетка.

Так же как и проницаемость сетки D, коэффициент усиления слабо зависит от режима, но при напряжении сетки, близком к запирающему, он снижается вследствие проявления «островкового» эффекта (см. рис. 9.9).

Уменьшение коэффициента усиления имеет место и при переходе в область положительных напряжений сетки, где его величина зависит не только от проницаемости сетки D, но и от процессов токораспределения. В связи с этим при положительных напряжениях сетки μ < 1/D. От напряжения накала коэффициент усиления почти не зависит.

Статические параметры триода μ, S, R_i связаны между собой простым соотношением. В соответствии с выражениями (9.31) и (9.37)

Возьмем приращения напряжений dU_c и dU_а такими, что dI_a=0, т. е.

Тогда

Отсюда в соответствии с формулой (9.38) находим, что

μ = SR_i(9.40)

Определение параметров по характеристикам

Заменим бесконечно малые приращения в формулах, определяющих параметры триода, малыми конечными приращениями:

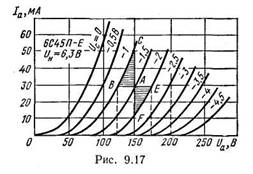
Эти приращения можно найти по характеристикам, для чего через точку А (рис. 9.17), в которой должны быть вычислены параметры, проводят вертикальную и горизонтальную линии до пересечения с соседней характеристикой. Полученные отрезки АВ и АС определяют приращения ∆U_a и ∆I_а. Приращение ∆U_с находят как разность напряжений сетки, при которых сняты рассматриваемые соседние характеристики. Поделив затем найденные приращения одно на другое в соответствии с соотношением (9.41), получим параметры данной лампы.

Определяемые по характеристикам величины представляют собой усредненные значения параметров в некотором интервале изменения переменных. Чем меньше приращения величин, тем ближе найденные значения параметров к истинным. Для получения более точных результатов необходимые для расчета приращения следует брать в обе стороны от заданной точки (т. е. и по ∆AEF).

Батушев В. А. Электронные приборы. М.: Высшая школа, 1980

Часть [1]  [2]  [3]  [4]  [5]  [6]  [7]  [8]  [9]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Это интересно

Проводимость триода на высокой частоте. С ростом частоты ста­новится значительной роль емкостных токов. Поэтому при анализе работы триода на высоких частотах нужно учитывать его между­электродные емкости: сетка — катод (С_ск), анод — катод (С_ак) и анод — сетка (С_ас). Междуэлектродные емкости триода зависят от размеров электродов и расстояний между ними, а также от длины вы­водов, их взаимного положения и степени экранирования. В маломощ­ных триодах они составляют 1—10 пФ, в мощных триодах, размеры электродов у которых значительно больше, емкости доходят до 50— 100 пФ.
    Величины емкостей изменяются в небольшой степени при прогре­ве лампы вследствие изменения размеров электродов, расстояний меж­ду ними и диэлектрической проницаемости изоляторов. Емкости за­висят от объемного заряда в лампе, изменяю­щего распределение потенциала в междуэлектродном пространстве. Наиболее сильно изменяется емкость сетка—катод, которая при включении накала может возрасти на 40—50%. Эта емкость существенно зависит и от напряжения сетки (рис. 9.18). При повышении отрицательного напряжения сетки происходит перераспределение объемного заряда на участке сетка—катод, его величина уменьшается, поэтому емкость С_ск падает.
    Емкость сетка—катод С_ск создает реак­тивную проводимость ώ С_ск во входной цепи, она является главной составляющей входной емкости лампы.
    Емкость анод — катод С_ак вызывает появле­ние реактивной проводимости ώ С_ак в выходной цепи и является основной составляющей выходной емкости лампы.
    Емкость анод—сетка С_ас обусловливает связь между входной и выходной цепями лампы, поэтому ее называют проходной емкостью. На высоких частотах, когда становится заметным влияние рассмот­ренных емкостей на работу лампы, проводимости триода перестают быть чисто активными, как на низких частотах, и становятся комплекс­ными величинами. Обозначив для удобства входные ток и напряжение индексом 1, а выходные — индексом 2, по аналогии с (5.4), (5.5) мож­но записать уравнения, связывающие малые гармонические колеба­ния напряжений и токов в триоде на высоких частотах:   I₁=Y₁₁U₁+Y₁₂U₂(9.42)
  I₂=Y₂₁U₁+Y₂₂U₂
    Влияние междуэлектродных емкостей на усилительные свойства триода. Входная емкость приводит к появлению реактивной составляющей входного тока, дополнительно нагружающей источник сиг­нала, а также может влиять на настройку резонансных цепей на вхо­де; все это отрицательно сказывается на эффекте усиления.
    Выходная емкость, уменьшая эквивалентное сопротивление на­грузки лампы на высокой частоте, снижает коэффициент усиления тем сильнее, чем выше рабочая частота. Этим ограничивается широкополосность усилителя [см. выражение (10.14)].
    Проходная емкость оказывает наиболее сильное влияние на свой­ства триода на высоких частотах. Через нее из выходной цепи во вход­ную проходит ток, создающий дополнительное переменное напряже­ние на сетке, пропорциональное выходному напряжению.
    При определенных условиях, зависящих от характера нагрузки, дополнительное сеточное напряжение совпадает по фазе с подводимым напряжением и в лампе возникает самовозбуждение, ее нормальная работа нарушается. Как показывается в теории усилителей, предель­ная частота, до которой триод может быть использован при заданном коэффициенте усиления К_u...
    Далее...