Это интересно

В последующих разделах рассмотрение вопроса о влиянии асимптотических характеристик на ограничение допустимой величины обратной связи будет основываться на соотношениях несколько более общих, чем соотношения между характеристикой идеального среза и асимптотой, определяемые кривыми фиг. 345 и 346. Но даже то упрощенное представление, которое может быть получено на основании изучения этих фигур, оказываемся достаточным для выяснения важной роли, какую асимптотические характеристики играют в вопросах проектирования. Очевидно, что большую величину обратной связи не удается получить в том случае, когда асимптота пересекает линию нулевого усиления слишком близко к области рабочего диапазона или же тогда, когда асимптота имеет слишком большую крутизну.
    К счастью, асимптотические характеристики могут быть относительно легко построены, так как они зависят только от паразитных параметров и, может быть, еще от некоторых других элементов схемы. Таким образом, эту характеристику можно вычислить с помощью упрощения действительной схемы. Во избежание напрасной потери времени, которую могло бы повлечь за собой выполнение практически неосуществимого варианта обратной связи, подобный расчет асимптоты желательно сделать как можно раньше, во всяком случае до того, как сделан подробный расчет усилителя.
    Вообще говоря, асимптотические характеристики определяются отчасти емкостями ламп и межкаскадных элементов, а отчасти — входной и выходной цепями и самой β-цепью. Подобное разделение, естественно, возникает в связи с рассмотрением вопроса о схеме фиг. 343. Приведенная там схема относится к предельному случаю, для которого влияние входной, выходной и β-цепи на асимптотическую характеристику снижено до нуля благодаря упрощению схемы усилителя в целом. Задача, стоящая перед инженером при проектировании, значительно шире, чем та, которая связана с созданием схемы, имеющей заданную асимптотическую характеристику. Общее решение, которое будет получено, отчасти зависит от вида обратной связи, а отчасти от того, каким образом разрешается вопрос о получении достаточно сильной обратной связи при соответствующих значениях прочих параметров, усилителя.
    Указанные соображения удобнее всего пояснить, возвращаясь к вопросу об асимптотических характеристиках, который мы разберем для случая простых схем, уже рассмотренных ранее. Если мы начнем с усилителей с обратной связью по напряжению, то в качестве типичной схемы можно выбрать схему фиг. 344.
    На фиг. 347 показана соответствующая предельному случаю асимптотическая цепь перехода от анода последнего каскада к сетке первого каскада. Наличие входных и выходных трансформаторов в схеме можно учесть добавлением параллельно конденсаторам C1 и С4 емкостей, эквивалентных распределенным емкостям обмоток. Чтобы схема обладала наибольшей эффективностью, эти дополнительные емкости должны быть невелики. Если мы будем, однако, стремиться сделать их слишком малыми, например, за счет уменьшения числа витков обмоток, то можем ухудшить другие параметры схемы.
    В нашей "асимптотической" схеме β-цепь представлена последовательно включенными емкостями С5 и С6. Для получения максимальной обратной связи величина этих емкостей должна быть взята значительной. В сущности говоря, их емкость может быть взята сколь угодно большой, так как при любой величине потерь в β-цепи, уменьшая величину сопротивления в токовой цепи обратной связи Т-образной схемы фиг. 344, мы получим также уменьшение на соответствующую величину сопротивления цепи, относящейся к обратной связи по напряжению. Однако, если величина сопротивления β-цепи будет сделана очень малой, то в пределах рабочей полосы может проявлять себя ее шунтирующее влияние на входную и выходную цепи усилителя.
    Простая схема усилителя с обратной связью по току приведена на фиг. 348. Для нее асимптотическая цепь от анода лампы на выходе схемы к входной сетке показана на фиг. 349. Емкость С7 может рассматриваться как распределенная емкость на землю β-цепи, а также входного и выходного трансформаторов. Желательно, чтобы эта емкость была возможно меньше. Две последовательно включенные емкости С 1 и С6 характеризуют емкость тех обмоток трансформаторов, которые имеют большее число витков. Наибольшая асимптотическая передача может быть получена в том случае, когда эти емкости имеют значительную величину. С другой стороны, соотношения показывают, что наивысший уровень коэффициента пассивной передачи и внешнего усиления можно получить, если обе эти емкости настолько малы, насколько это возможно. Таким образом, и в этом случае вид асимптотической характеристики определяется тем, каким образом был достигнут компромисс между отмеченными выше соображениями и соображениями, относящимися к обратной связи, хотя надо сказать, что детали этого вопроса несколько отличаются от того, что мы имели в случае усилителя с обратной связью по напряжению.
    Далее...

Максимально возможная обратная связь

Анализ, который был проведен в связи со схемой фиг. 345, показывает, почему асимптотическая характеристика ограничивает величину обратной связи, которая может быть достигнута, однако он не дает точного ответа на вопрос, какая величина обратной связи может быть получена при данной асимптоте. Как уже указывалось, результирующая фазовая характеристика достигает предельного значения 180° лишь в точке пересечения, в то время как на всех более низких частотах имеет место различная величина запаса по фазовому сдвигу. Соотношение между величиной запаса по фазовому сдвигу и степенью обратной связи, которое было приведено раньше, показывает, что несколько более выгодные результаты для крайнего случая могут быть получены, если предельное значение 180° будет достигнуто за пределами области среза. Можно получить требуемую фазовую характеристику, если учесть, что исходная характеристика идеального среза связана с асимптотой несколько более сложным образом, чем в рассмотренном выше случае.

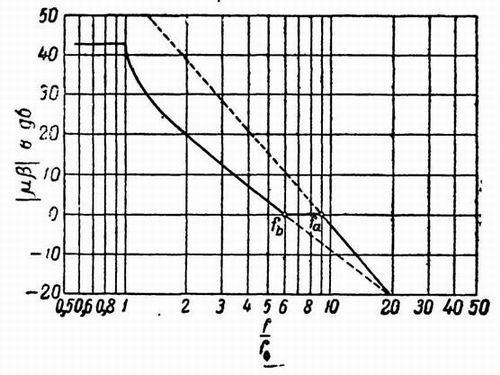
Фиг. 351

На фиг. 351 приведена общая характеристика среза. Она состоит из исходной теоретической характеристики, построенной при условии, что у = 0 для области, лежащей между краем полосы и точкой f_b, соответствующей пересечению характеристики с линией нулевого усиления, из отрезка f_bf_a, на котором точка f_a определяет пересечение линии нулевого усиления с асимптотой, и, наконец, из самой асимптоты. Можно считать, что эта характеристика составлена из характеристики идеального среза, продолженной до бесконечности, и из двух наклонных полупрямых. Одна из этих полупрямых начинается в точке f_b и имеет положительную крутизну в 12 дБ на октаву, так как характеристика идеального среза относилась к предельному значению у. Другая начинается в точке f_a и имеет отрицательную крутизну, равную крутизне самой асимптоты. Как видно из уравнения (15.12), фазовая характеристика, соответствующая наклонной полупрямой, в области низких частот линейна. Величина фазового сдвига, определяемая двумя дополнительными полупрямыми, будет изменяться таким же образом, а так как они имеют крутизну противоположного знака, то результат можно получить, производя вычитание, при условии, конечно, что постоянные, определяющие величину масштаба по осям, выбраны соответствующим образом.

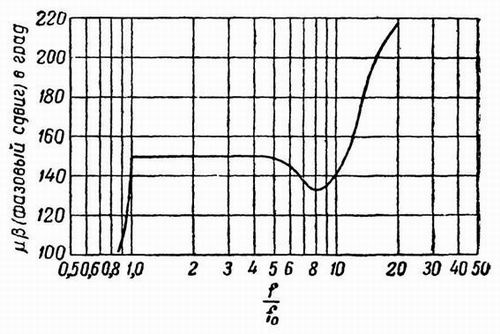
Фиг. 352

Очевидно, что правильное соотношение можно получить в том случае, когда отношение частот для тех точек, из которых начинаются полупрямые, равно отношению крутизн этих полупрямых. Если мы обозначим через п крутизну асимптоты, взятую в единицах, соответствующих 6 дБ на октаву, то величина f_b может быть выражена через f_a с помощью соотношения

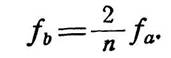(18.6)

Например, на фиг 351, где крутизна асимптоты равна 18 дБ на октаву, отношение частот равно 18:12 или 3:2. При этом на нижних частотах результирующая фазовая характеристика будет совпадать с первоначальной идеальной кривой. На верхних частотах, где линейная аппроксимация фазовой характеристики полубесконечной наклонной прямой недостаточно точна, указанные составляющие будут иметь известное значение. Однако, как видно из фиг. 352, угол фазового сдвига получается меньше 180° в точке, соответствующей пересечению характеристики усиления с нулевой линией. Таким образом, устойчивость схемы обеспечена.

После того как величина f_b найдена, нетрудно определить, насколько значительной может быть обратная связь в пределах полосы. Для этого достаточно во всей области, от края полосы до частоты f_b, сбросить по 12 дБ на октаву и добавить к полученному результату еще 12 дБ с тем, чтобы принять во внимание увеличение крутизны характеристики среза у края полосы. Основываясь на соотношении получим:

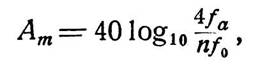(18.7)

где f₀ соответствует краю полосы, а А_т определяет величину обратной связи в децибелах в пределах полосы. Если обратная связь, определяемая (18.7), больше той, которая требуется для всего усилителя в целом, то ее излишек можно использовать для получения характеристики среза, соответствующей таким величинам усиления и фазового сдвига, какие позволяют избежать самовозбуждения.

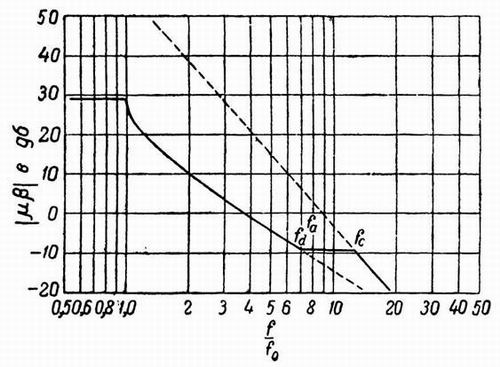
Фиг. 353

В качестве иллюстрации этого положения на фиг. 353 и 354 приведены соответствующие кривые, построенные для величины усиления и фазового сдвига х = 9 и у = ¹/₆.

Величина запаса по углу фазового сдвига у = ¹/₆ (что соответствует 30°) относится к характеристике идеального среза, имеющей крутизну в 10 дБ на октаву, как и до сих пор. Запас по величине усиления характеризуется тем, что горизонтальная часть характеристики, связывающая идеальный срез с асимптотой, опущена на соответствующую величину ниже уровня нулевого усиления. Как и прежде, предполагается, что отношение частот, с которых начинаются полупрямые, такое же, как и отношение крутизн этих прямых, так что полученная фазовая характеристика в области среза совершенно аналогична идеальной характеристике.

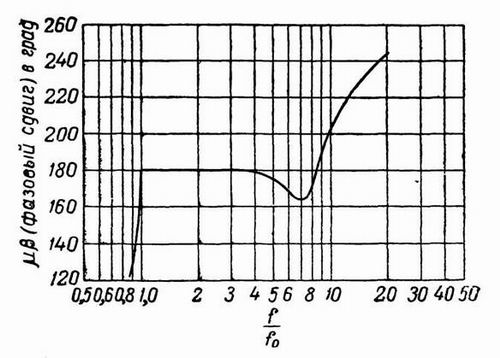
Фиг. 354

Таким образом, очень просто подсчитать, на сколько нужно уменьшить величину обратной связи для получения требуемого запаса по величине усиления и фазового сдвига. Приступая к подобному расчету, частоту f_с, которая на фиг. 353 соответствует точке пересечения с асимптотой, следует выразить через частоту f_a при помощи крутизны асимптоты и запаса по усилению х. Так как крутизна асимптоты равна 6 п дБ на октаву, что соответствует 20 п дБ на декаду (т. е. для соотношения частот 10:1), то очевидно, что мы получим f_c/f_a = x/20n, или, другими словами, f_c = 10^x/20nf_a. В то же время крутизна идеального среза соответствует 12 (1 — у) дБ на октаву или 40(1—у) дБ на декаду. Таким образом, мы имеем соотношение между величинами крутизны и частотами, находящимися на границе горизонтальной части характеристики, которое дает f_d = [2(l — y)/n]f_c. Наконец, известные соотношения, относящиеся к идеальному срезу, показывают, что обратная связь на краю полосы f₀ должна быть больше, чем на частоте f_d, на 40(1 — y)log₁₀2f_d/f₀ дБ. Однако эта разница равна А+х, где Л —величина обратной связи в пределах полосы.

Суммируя полученные результаты, мы можем написать:

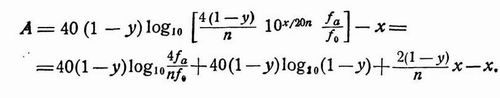(18.8)

Так как у представляет собой малую величину, то мы можем разложить log₁₀(l —y) в степенной ряд и пренебречь членами, в которые у входит в степени выше первой. Это позволяет в соотношении (18.8) член 40(1—y)log_l0(1— у) заменить на —17,4y. Если мы, кроме того, на основании (18.7) заменим 40log₁₀4f_a/nf₀ на А_т , то получим следующее окончательное выражение:

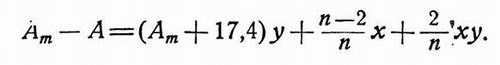(18.9)

Так как последний член правой части обычно имеет малую величину, то общее уменьшение величины обратной связи может рассматриваться как сумма уменьшений за счет отдельно взятых величин запаса по фазовому сдвигу и по усилению. Примером применения полученного соотношения может служить сопоставление кривых фиг. 351 и 353. В обоих случаях асимптотическая частота f_a была принята равной 9f₀. Согласно соотношению (18.7), при этом можно получить величину обратной связи не больше, чем 43 дБ, что как раз соответствует обратной связи, указанной на фиг. 351. В то же время величина обратной связи, которая характеризуется фиг. 353, составляет только 29 дБ. Из общей разности в 14 дБ около 10 дБ относится к тому члену соотношения, который определяет запас по фазовому сдвигу, около 3 дБ — к члену, определяющему запас по усилению и примерно 1 дБ к последнему члену с ху.

Часть [1]  [2]  [3]  [4]  [5]  [6]  [7]  [8]  [9]  [10]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

Левзея и экдистерон в спорте, бодибилдинге и медицине

Качественный электромонтаж

Система поддержки мобильной торговли Моби-С

Качественные электромонтажные работы

Это интересно

Если мы хотим построить характеристики среза того вида, который соответствует фиг. 351, то для различных типов усилителей нам придется пользоваться несколько различными методами. Возможности, которые имеются в этом отношении, будут рассмотрены в этой главе несколько ниже. В следующей главе будут приведены примеры, подробно иллюстрирующие методы проектирования. Однако возможно сделать одно замечание общего характера, которое может быть отнесено к громадному большинству случаев проектирования усилителей. Если в усилителе, выполненном наиболее простым путем, без учета формы характеристики среза, мы имеем горизонтальную характеристику обратной связи в пределах рабочей полосы, то эта форма характеристики будет иметь тенденцию сохраниться и в некоторой области за пределами полосы. Такое положение имеет место, во всяком случае, для некоторой части схем. Однако на высоких частотах характеристика имеет спад за счет влияния паразитных элементов схемы. По мере повышения частоты паразитные параметры сказываются все более заметным образом, причем в конце концов общая характеристика петли обратной связи принимает асимптотический вид. В этом случае характеристика любой схемы полностью определяется только одними паразитными элементами. Таким образом, полная характеристика петли обратной связи имеет вогнутость во внутрь, если не во всей области среза, то, во всяком случае, на высоких частотах. В то же время характеристика среза, изображенная на фиг. 351, имеет вогнутость наружу. Следовательно, основная задача при проектировании большей части усилителей заключается в том, чтобы в петлю обратной связи внести такие потери, чтобы степень среза возрастала на частотах, незначительно отклоняющихся от частот рабочей полосы, и в то же время уменьшалось бы на более высоких частотах. Это эквивалентно такому уменьшению влияния паразитных параметров, при котором они уже не сказываются на характеристике петли обратной связи до тех пор, пока эта характеристика не пересекается с асимптотой.
    В качестве крайнего случая рассмотрим схему, изображенную на фиг. 355. Предполагается, что система представляет собой простой полосовой усилитель, в котором во входной и выходной цепях, а также в качестве межкаскадных элементов используются зашунтированные сопротивлениями резонансные контуры. Примем, что все контуры имеют одинаковую величину Q. Если воспользоваться соотношениями для фильтров нижних частот, то уравнение для характеристики петли можно записать как 140 (1+0,287iω)4. Коэффициенты в этом выражении выбраны таким образом, чтобы было удобно вести сравнение с результатами, приведенными на фиг. 351. Здесь получается такая же величина усиления на нижних частотах и та же асимптота, что и на указанной фигуре. Характеристика усиления петли для рассматриваемого устройства изображена в виде кривой I на фиг. 356, а теоретическая характеристика среза фиг. 351 дана кривой II. Таким образом, разность между этими кривыми, показанная в виде заштрихованной площади/соответствует величине потерь, которые должны быть внесены в петлю обратной связи с помощью выравнивающих контуров или же каких-либо аналогичных устройств с тем, чтобы стабилизировать схему.
    Результаты, которые при этом получаются, можно усмотреть на основании сравнения фазовых характеристик, показанных в виде кривых I и II фиг. 357. Площади, ограниченные этими кривыми, равны между собой, однако внесение дополнительных потерь приводит к такому перераспределению общей площади, что максимальная величина фазового сдвига остается меньше 180° в более широком интервале частот. Из чертежа видно, что исходная фазовая характеристика пересекает линию 180° на частоте f=3,5f0. Если схема стабилизирована введением регулировки усиления, с помощью которой в этой точке усиление канала уменьшено до нуля, то результирующая величина обратной связи в пределах рабочей полосы будет равна 12 дБ. Для теоретических характеристик среза соответствующая величина равна 43 дБ. Примерно половину от разности в 30 дБ для дополнительной обратной связи можно получить, если на фиг. 356 заменить кривую I прямой линией с соответствующим образом подобранной крутизной. Увеличение крутизны теоретической характеристики непосредственно за краем рабочей полосы соответствует приращению на 12 дБ, а для горизонтальной части результирующей кривой непосредственно перед пересечением с асимптотой — приращению на 5 или 6 дБ. Далее вопросы расчета, относящиеся к подобным случаям, рассмотрены более подробно.
    Далее...