Это интересно

В многополосных АС головки, предназначенные воспроизводить разные части частотного диапазона, включаются через так называемые разделительные фильтры. Их назначение заключается в том, чтобы пропускать к каждой головке напряжение только нужных частот. Эти фильтры различают по крутизне спада за пределами высшей или низшей граничной частоты. Обычно применяют фильтры с крутизной спада 6, 12 или 18 дБ на октаву. По схеме их разделяют на фильтры для двухполосных и трехполосных АС. Исходными данными для расчета являются частота раздела и сопротивление головки в рабочей полосе фильтра. На рис. 89,а, б, в приведены схемы фильтров с крутизной спада соответственно 6, 12 и 18 дБ/октава. В верхней части каждого из рисунков приводится схема фильтра для двухполосной АС, а в нижней — для трехполосной. На каждом рисунке приведена также формула для определения элементов этих, фильтров. Емкости, индуктивности и сопротивления соответственно даны в фарадах, генри и Омах. Конденсаторы фильтров выбирают из номенклатуры выпускаемых промышленностью изделий. Больше всего подходят для разделительных фильтров конденсаторы типа МБГО.
    Что касается катушек индуктивности, то их изготавливают путем намотки без железного сердечника во избежание искажений, обусловленных перемагничиванием. Практически оптимальная в смысле максимума отношения индуктивности катушки к ее активному сопротивлению конструкция получается, когда внутренний диаметр цилиндрической обмотки вдвое больше ее высоты h, a внешний диаметр в 4 раза больше h и в 2 раза больше внутреннего диаметра. При этих условиях значение h= √L/R/0,866 мм (L, мкГн, R, Ом), длина провода l= 187,3√Lh, число витков N = 19,88 √L/h, диаметр провода (без изоляции) d = 0,84·h/√N мм, масса провода т = (h3/21,4) ·103 кг.
    Пример. Определить данные катушки индуктивностью 3,37 мГн разделительного фильтра, нагруженного головкой сопротивлением 15 Ом. Активное сопротивление рассчитываемой катушки выбираем равным 5% от сопротивления головки. Это соотношение можно считать вполне приемлемым. Тогда R = 0,05 -15 = 0,75 Ом, откуда L/R = 3,37·103/0,75 =4500. Высота обмотки h= √4500/0,866= 24,5 мм, длина провода l = 187,3 √ 3,37·103·24,5 = 5,35·104 мм = 53,5 м, число витков N = 19,88 √ 3,37·103/24,5 = 233 витка, диаметр провода d = 0,84·24,5/ √ 233 = 1,35 мм, масса провода m = (24,53/21,4) ·103 = 0,69кг.
    Естественно, полученные числа должны быть округлены, и в первую очередь диаметр провода, до ближайшего стандартизованного диаметра. Окончательно индуктивности подгоняют путем измерения на мостике, отматывая по нескольку витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным. Катушки можно наматывать на пластмассовые, деревянные или картонные каркасы. Применяется и бескаркасная намотка (рис. 90), для того чтобы катушка не развалилась, витки после намотки каждого слоя промазывают клеем БФ-4. Если есть возможность, то для полимеризации клея катушку запекают в термостате при температуре 140—160° С в течение 1 ч. Если такой возможности нет, то катушка должна быть высушена при комнатной температуре в течение суток. Иногда провод, в качестве которого предпочитают марку ПЭЛ, бывает покрыт каким-либо маслом. Тогда перед намоткой или в ее процессе провод нужно протереть ваткой, смоченной смесью из 50% спирта и 50% бензина или, в крайнем случае, чистым бензином. Собранный и смонтированный фильтр, т. е. его конденсаторы и катушки, размещают на полочке, укрепленной внутри корпуса АС. Разумеется, все электрические соединения должны быть хорошо пропаяны во избежание шорохов и тресков, могущих возникнуть из-за плохих контактов.
    В предыдущих разделах мы ознакомились с основными параметрами, которые характеризуют работу АС. Эти параметры определяются с помощью соответствующих измерений, которые могут быть разделены на две основные группы: электроакустические и электрические.
    Далее...

Элементарная теория схем с обратной связью

В простейшем виде усилитель с обратной связью может быть представлен как совокупность обычного усилителя, или μ-цепи, и пассивного четырехполюсника, или β-цепи, при помощи которого часть энергии с выхода системы может быть подана обратно на вход. Подобная комбинация изображена на фиг. 14. Обе цепи, μ и β, являются, само собой разумеется, четырехполюсниками и только ради простоты обозначены на фиг. 14 одной линией.

Если часть энергии с выхода возвращается обратно ко входу, в схеме, естественно, могут возникнуть паразитные колебания. В этом случае схема обычно не может работать как усилитель. Однако характеристики устройства могут быть легко определены, если мы предположим, что подобные колебания в схеме отсутствуют. Необходимо только учитывать, что процессы, происходящие как в μ- так и в β-цепях, полностью определяются напряжением на зажимах этих четырехполюсников. При этом можно не принимать во внимание, что последние являются частями замкнутой цепи обратной связи. Обозначим соответственно через Е₀ и E_R напряжение, подводимое от источника ко входу, и напряжение, снимаемое с выхода схемы, как это показано на фиг. 14. Пусть E₁ будет некоторое дополнительное напряжение, подаваемое β-цепью с выхода схемы на вход. Ввиду того, что μ-цепь работает как обычный усилитель, должно удовлетворяться уравнение

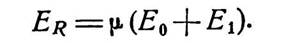(3.1)

Аналогично, если β является коэффициентом передачи β-цепи, то напряжение, подводимое к входным зажимам посредством обратной связи, может быть представлено в виде

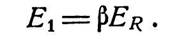(3.2)

Исключая Е₁ из этих двух уравнений, находим

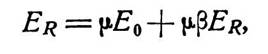(3.3)

или

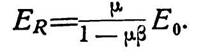(3.4)

При отсутствии β цепи выходное напряжение может быть записано в виде

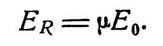
Отсюда следует приводимая ниже теорема:

Теорема. Обратная связь уменьшает коэффициент усиления усилителя в 1 — μβ раз.

Величина μβ может быть названа коэффициентом обратной связи.

Очевидно, что эта величина определяет коэффициент передачи напряжения по замкнутой петле от входа усилителя обратно к этому же входу. На практике обычно μβ значительна больше единицы. При этом уравнение (3.4) удобно переписать следующим образом

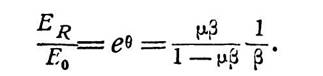(3.5)

Учитывая, что если μβ велико, то первый множитель в правой части (3.5) близок но абсолютной величине к единице, мы можем заключить, что коэффициент усиления усилителя примерно обратно пропорционален коэффициенту передачи (3-цепи или, другими словами, примерно пропорционален затуханию в β-цепи.

Получаемая при этом погрешность за счет отклонения | μβ/(l — μβ) | от единицы будет в дальнейшем называться μβ-погрешностью.

Из (3.5) следует, что на величину коэффициента усиления в значительной степени влияют небольшие изменения в β-цепи, в то время как изменения в μ-цепи почти не оказывают никакого действия. Чтобы последнее положение стало более ясным, продифференцируем (3.4), считая β постоянной величиной. Разделив затем обе части полученного уравнения на (3.4), имеем

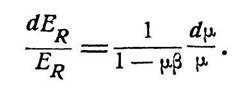(3.6)

В этом выражении величины dE_R/E_R и dμ/μ, очевидно, представляют соответственно изменения коэффициента усиления усилителя в целом и коэффициента усиления μ-цепи в случае, когда обе величины выражены в логарифмических единицах — неперах или децибелах. Отсюда следует теорема:

Теорема. Изменение общего коэффициента усиления усилителя (в дб) на каждый децибел изменения коэффициента усиления μ-цепи уменьшается обратной связью в
отношении (1 —- μβ):1.

Последнее свойство обратной связи является особо важным с точки зрения уменьшения действия помех или нелинейных искажений, возникающих в μ-цепи. В широком физическом смысле помехи, так же как и нелинейные искажения в некотором элементе схемы, могут рассматриваться как некоторые “изменения” в данном элементе. Чувствительность цепи к такого рода изменениям всегда находится в определенном соответствии с чувствительностью цепи к нормальным изменениям параметров данного элемента. Поэтому указанное свойство систем с обратной связью является следствием только что выведенной теоремы. Однако для того чтобы доказать это независимым образом, положим, что в каком-либо внутреннем звене μ-цепи включен генератор D₀, как показано на фиг. 15. D₀ может представлять собой напряжение помех, которые возникают за счет плохого контакта или фона переменного тока, либо напряжение, получающееся за счет нелинейных искажений в μ-цепи.

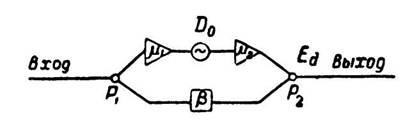
Фиг. 15

Обозначим через E_d выходное напряжение, обусловленное генератором шумов, а через D₁ — дополнительное напряжение, появляющееся между μ₁, и μ₂ благодаря связи по петле μβ. Учитывая, что общее напряжение в месте включения генератора равно D₀ + D₁ а коэффициент усиления между этим .участком и выходными зажимами схемы равен μ₂, мы можем .записать выражение для E_d в следующем виде:

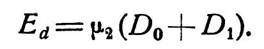(3.7)

Напряжение D₁ обусловленное обратной связью через β-цепь и цепь μ₁, очевидно, определится следующим образом:

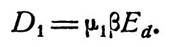(3.8)

Исключая D₁ получим:

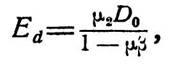(3.9)

где μ равно общему коэффициенту усиления усилителя μ₁μ₂. Принимая во внимание, что напряжение помех на выходе при отсутствии обратной связи равно μ₂D₀, получаем следующую теорему:

Теорема. Уровень помех на выходе усилителя понижается обратной связью в отношении (1 — μβ): 1.

Отсюда, конечно, не следует, что отношение сигнала к помехе увеличивается в то же число раз, так как обратная связь изменяет уровень сигнала в μ-цепи.

Чтобы выяснить, как влияет обратная связь на величину отношения сигнала к помехе, сравним наш усилитель с устройством без обратно связи, имеющим тот же результирующий коэффициент усиления μ/(l-μβ) и то же входное и выходное напряжения Е₀ и Е_R . Для облегчения сравнения положим, что μ-цепь усилителя с обратной связью разделена на два участка, μ₁ и μ₂ (фиг. 15), коэффициенты усиления которых соответственно равны 1 — μβ и μ/(1 — μβ). Ввиду того, что каскад μ₂ усилителя с обратной связью и усилитель без обратной связи, с которым мы производим сравнение, имеют одинаковые величины коэффициента усиления и одинаковые значения выходного напряжения, то очевидно, что уровни сигнала на выходе μ₂ и на входе усилителя без обратной связи будут также одинаковы. Следовательно, обратная связь наиболее эффективно улучшает отношение сигнала к помехам, если источник помех включен в μ-канал между μ₁ и μ₂.

С другой стороны, в части μ₁ уровни сигнала меньше, чем в любом месте сравниваемого усилителя без обратной связи; поэтому, если источник помех включен в этой части μ-цепи, то отношение сигнала к помехе будет улучшаться лишь частично.

На входных зажимах первой лампы, где величина сигнала понижается также в (1 — μβ) раз, обратная связь не дает никакого изменения величины отношения сигнала к помехе. Поэтому обратная связь является удобным методом борьбы с помехами, характерными для оконечных каскадов и обусловленными вторичной модуляцией, или фоном питающего переменного тока (например, в случаях применения ламп прямого накала). Помехи такого рода, однако, малы по сравнению с шумами, обусловленными термическими флюктуациями, дробовым эффектом и т. д., которые заметно сказываются в первых каскадах.

Обратная связь играет важную роль в радиотехнических устройствах, так как она позволяет в значительной степени уменьшить эффект, вызываемый фоном и изменением коэффициента усиления μ-цепи и т. д. Понижение общего коэффициента усиления при применении обратной связи является, естественно, недостатком последней и делает необходимым применение более сложной μ-цепи для получения заданной величины коэффициента усиления. Однако это обстоятельство не является столь серьезной жертвой, если учесть выигрыш, который при этом достигается.

Рассмотрим для примера усилитель с общим коэффициентом усиления во внешней цепи в 40 дБ и обратной связью также в 40 дБ. При этом μ-цепь должна иметь коэффициент усиления, равный 80 дБ, т. е. в два раза больше того коэффициента усиления в дБ, который соответствует отсутствию обратной связи. Таким образом, усложнив в два раза μ-цепь, получим повышение линейности и стабильности усиления в 100 раз.

Часть [1]  [2]  [3]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

WEB дизайн студия «Вектор»

Система автоматизации ERP NOVA

Торговые центры и франшизы

Это интересно

Типы схем с обратной связью
    Проще всего классифицировать схемы с обратной связью, выбирая в качестве основного критерия способ соединения μ- и β-цепей между собой, а также с входной и выходной внешними цепями. Чтобы показать возможность получения различных вариантов соединений, неудобно, конечно, пользоваться изображением μ- и β-цепей в виде одиночных линий, как это было сделано на фиг. 14, ибо эти цепи так же, как входная и выходная внешние цепи, являются двухпроводными. Учитывая это обстоятельство, мы приходим к схеме, изображенной на фиг. 16, где три цепи соединены между собой при помощи шестиполюсников. Классификация схем обратной связи определяется видом этих соединительных шестиполюсников. Представляется, конечно, возможным построить весьма большое число подобного рода устройств. Простейшие и в то же время наиболее часто употребляемые из них показаны на фиг. 17—21. Зажимы на каждой из этих фигур обозначены в соответствии с фиг. 16. На фиг. 17, например, показана схема обратной связи по току. Здесь μ-цепь представляет обычный трехкаскадный усилитель, междукаскадные импедансы которого обозначены через I1 и I2. Цепь β представлена в виде П-образного соединения ветвей A, В и С. В частном случае число ветвей может быть уменьшено до одной. В других случаях β-цепь может иметь более сложную конфигурацию. Зажимы входной и выходной цепей e—f и e´—f´ соответствуют обмоткам трансформаторов, подключенных к лампам. В этом случае трансформаторы и внешние цепи не входят в общую схему и должны быть учтены дополнительно.
    Характерной особенностью данного усилителя является то, что μ- и β-цепи соединены между собой на обоих концах усилителя последовательно, если смотреть со стороны внешних цепей.
    На фиг. 18 показана схема обратной связи по напряжению.
    Здесь β-цепь взята типа T, но, как и в предыдущем случае, она может представлять любой четырехполюсник.
    В этой схеме, как легко видеть, μ- и β-цепи, а также внешние цепи как на входе, так и на выходе усилителя включены параллельно друг другу. Схемы обратной связи по току и по напряжению являются простейшими, но в то же время для большинства случаев, вероятно, наиболее удобными устройствами. Помимо того, эти схемы позволяют обычно получить максимальную величину обратной связи. Однако, с другой стороны, этим схемам присущи два важных недостатка.
    Первый из них заключается в том, что за счет обратной связи сопротивления усилителя, измеренные со стороны внешних цепей, становятся либо очень большими, либо очень малыми. Поэтому эти схемы непригодны в тех случаях, когда необходимо получить удовлетворительную величину коэффициента отражения от внешней цепи. Вторым недостатком приведенных схем является то обстоятельство, что сопротивления внешних цепей представляют собой части μβ-канала. Поэтому изменение сопротивлений внешних цепей может влиять на μβ-характеристики, что приводит к неустойчивости схемы.
    Эти недостатки можно устранить применением мостовой схемы обратной связи, изображенной на фиг. 19. Данная схема содержит три новых ветви, обозначенных через Z2, Z3 и Z4 и включенных на каждой стороне усилителя. Четвертая ветвь, Z1, позволяет регулировать, если это необходимо, входное и выходное сопротивления μ-цепи.
    Три новых ветви совместно с сопротивлениями μ- и β-цепей, а также внешних цепей, образуют устройство, имеющее в общей сложности шесть ветвей. Если какую-либо из этих ветвей представить как сопротивление генератора, то остальные пять ветвей дадут четыре плеча моста и диагональную ветвь. Например, если в качестве сопротивления генератора взять внешнюю цепь, то в диагональ оказывается включенным сопротивление β-цепи.
    Далее...