Это интересно

В вопросе, который сейчас нами рассматривается, существенно требование о том, чтобы усиление по петле обратной связи уменьшалось от значительной величины, соответствующей обычной полосе частот, до нуля или даже ниже на достаточно высоких частотах. При этом величина фазового сдвига не должна превышать некоторого заданного значения. Из общих соображений, приведенных ранее, следует, что это требование определяет, насколько резко должно уменьшаться усиление за пределами полосы. Если бы не было ограничений, обусловленных фазой, то было бы желательно, чтобы усиление уменьшалось очень резко. Чем резче убывает величина обратной связи, тем более узкой может быть взята та область, в которой требуется соблюдение условий, обеспечивающих отсутствие самовозбуждения.
    Более того, желательно, чтобы срез характеристики имел место как можно раньше с тем, чтобы избежать трудностей, связанных с влиянием паразитных параметров на высоких частотах. Однако анализ, приведенный ранее, показывает, что фазовый сдвиг примерно пропорционален степени изменения усиления. Следовательно, если фазовый сдвиг не должен превосходить определенной величины, то и частота, начиная с которой появляется срез, не может превышать определенного предела. Например, если мы примем величину запаса по фазовому сдвигу равной 30°, то допустимый сдвиг по фазе μβ будет 150°, что примерно соответствует изменению величины усиления в 10 дБ на октаву.
    Ясно, что желательно иметь в заданных пределах возможно большую допустимую величину фазового сдвига с тем, чтобы обеспечить возможно более резкий срез характеристики. Точная форма среза, которая наилучшим образом удовлетворяет этому условию, может быть найдена, если мы обратимся к анализу, связанному с соотношением, определяющим максимальную величину усиления межкаскадной цепи. Напомним, что это соотношение было получено из общей формулы в предположении, что усиление межкаскадной цепи постоянно в рабочей полосе и что фазовый угол за пределами полосы также постоянен и равен — π/2. Совершенно аналогичная аналитическая задача возникает и в данном случае, если требуется получить постоянную обратную связь в рабочей полосе.
    Требования, относящиеся к усилению вдоль петли обратной связи, здесь должны заменить собой те требования, которые были установлены к усилению межкаскадной цепи, в то время как за пределами полосы требование о том, чтобы фазовый сдвиг по петле обратной связи не превышал известной величины, должно заменить собой соответствующие требования в отношении фазового угла межкаскадной цепи. Единственное различие заключается в том, что требования к фазовому углу должны соответствовать (1 —у)π радиан, взамен π/2 радиан. Следовательно, мы можем переписать те выражения, которые мы имели для усиления межкаскадной цепи и фазового сдвига применительно к цепи обратной связи, в следующем виде:
    где А и В представляют собой соответственно вещественную и мнимую составляющие величины ln T=ln(—μβ), a A0 определяет усиление по петле в рабочей полосе частот.
    Наиболее существенные результаты в этом отношении заключаются в следующем:
    1. Для случая межкаскадных элементов кривая, характеризующая зависимость усиления от lgω, переходит на высоких частотах в прямую с крутизной 6 дБ на октаву. Эта прямая соответствует характеристике, определяемой одной лишь паразитной емкостью.
    В рассматриваемом сейчас случае точно так же кривая, соответствующая уравнению (18.1), переходит в прямую линию, имеющую крутизну, равную 12(1—у) дБ на октаву. Это показано пунктирной линией на фиг. 342. У края полосы действительная кривая будет спадать по закону, более резкому, чем прямая линия, если мы примем во внимание, что в пределах полосы крутизна характеристики равна нулю, а на краю полосы она лежит на 12(1—у) дБ выше прямой. Это соответствует выигрышу 6 дБ, который дает межкаскадный элемент с плоской формой характеристики усиления на краю полосы по сравнению с характеристикой, определяемой одной емкостью. Благодаря этому возникает возможность выиграть целую октаву в области интервала среза.
    Далее...

Асимптотические характеристики петли обратной связи

Непосредственная аналогия между характеристиками межкаскадного усиления и коэффициентом передачи вдоль петли обратной связи оказывается нарушенной только в одном существенном пункте. В случае межкаскадных цепей очевидно, что предел абсолютного уровня усиления определяется тем обстоятельством, что на достаточно высоких частотах характеристики усилителя вырождаются в характеристики чисто емкостной нагрузки. Если усиление в рабочей полосе будет очень велико, то окажется невозможным уменьшить усиление за пределами полосы настолько, чтобы оно совпадало с усилением, определяемым чисто емкостной нагрузкой, без получения сдвига по фазе, превышающего 90°.

В задачах, относящихся к коэффициенту передачи по петле обратной связи, абсолютный уровень усиления, который может быть получен в рабочей полосе, оказывается ограниченным условиями, сходными с предыдущими, но более сложными. Если исходить из чисто теоретических соотношений, аналогичных (18.1), то ясно, что не существует никаких обстоятельств, которые в этом отношении ограничивали бы величину обратной связи. Если, однако, постоянная Л_о, определяющая величину обратной связи в рабочей полосе частот, будет возрастать, то область, в пределах которой имеет место заметная величина коэффициента передачи, начнет расширяться в сторону все более и более высоких частот. Ограничение наступает в том случае, когда частота становится столь высокой, что паразитные параметры определяют поведение системы и не дают возможности получить с достаточной точностью те результаты, которые соответствуют уравнению (18.1). Например, мы, очевидно, встречаемся с затруднениями в том случае, когда соотношение (18.1) определяет усиление вдоль петли обратной связи при столь высокой частоте, что лампы, работающие лишь на собственные межэлектродные емкости, не могут обеспечить усиление. Этот предельный случай, который осуществляется в рассмотренной нами специальной схеме фиг. 343, является одной из причин возможности использования этой схемы при расчетах для сравнения с ней других схем. В практических схемах усилителей ограничения в усилении по петле обратной связи возникают раньше, вследствие наличия дополнительных потерь в величине коэффициента передачи по петле, за счет входной и выходной цепей, а также β-цепи.

В сравнении со случаем межкаскадного усиления основное различие, которое должно быть отмечено, заключается здесь в том, что коэффициент передачи на высоких частотах зависит от целого комплекса причин, а не от одной лишь величины собственной паразитной емкости. Характеристика, которая определяет величину передачи по петле обратной связи на достаточно высоких частотах при учете действия всех паразитных параметров петли, будет в дальнейшем называться асимптотической характеристикой петли. На примере схемы, приведенной на фиг. 344, легко понять, как можно рассчитать такую асимптотическую характеристику. Схема представляет собой усилитель с обратной связью по напряжению. Система относится к Т-образному типу и образуется цепями N₅, N₆ и N₇. Входная и выходная цепи представлены элементами N₁ и N₄ , а межкаскадные сопротивления — элементами N₂ и N₃. Конденсаторы С представляют собой паразитные емкости, за исключением конденсаторов С₅ и С₆, которые могут рассматриваться как емкости, введенные в схему для шунтирования сопротивлений N₅ и N₆ с тем, чтобы на высоких частотах получить необходимую величину передачи с выхода на вход. На достаточно высоких частотах величина передачи по петле обратной связи будет определяться только величиной этих емкостей, независимо от значения N. Таким образом, если обозначить крутизны ламп через G_m1 G_m2 и G_m3, то асимптотические значения усиления для первых двух ламп будут G_m1/ωC₂ и G_m2/ωC₃. Оставшаяся часть петли обратной связи будет включать в себя третью лампу и потенциометр, составленный из емкостей С₁, С₄, С₅ и С₆. Асимптотическую величину усиления можно записать в виде G_m3/ωC, где величина полного асимптотического усиления будет представлять собой произведение всех этих величин или, другими словами, будет равна G_m1 G_m2 G_m3/ω³ C C₂ C₃.

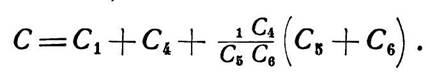(18.3)

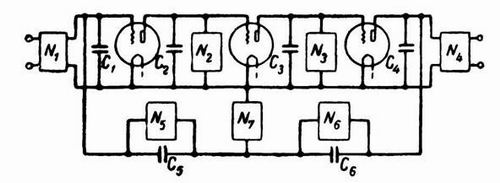
Фиг. 344

Если изобразить зависимость величины асимптотического усиления от частоты в логарифмическом масштабе, то мы получим прямую линию с наклоном в 18 дБ на октаву. В том, что указанная асимптота при логарифмическом масштабе будет представлять собой прямую линию для самого общего случая, можно убедиться, записав выражение для сопротивления передачи вдоль петли обратной связи в виде

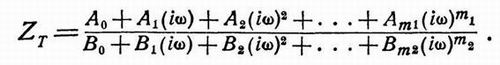(18.4)

Когда ω приближается к бесконечности, предыдущее выражение дает:

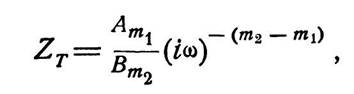(18.5)

что определяет собой прямую линию с наклоном в (m₂ — m₁) условных единиц на октаву, причем каждая из условных единиц соответствует 6 дБ.

В дальнейшем величину (m₂ — m₁) мы будем обозначать через п. На фиг. 344 n = 3, что соответствует числу ламп в схеме. Очевидно, что п не может быть меньше, чем число ламп, так как каждая из ламп во всяком случае будет работать на собственную паразитную емкость, в то время как в некоторых схемах эта емкость, входящая в нагрузку, может быть и больше. Например, если устранить емкость С₅ или C₆ на фиг. 344 и считать, что элементы N₅ или N₆ являются сопротивлениями, то асимптота получит наклон, соответствующий 4 условным единицам, и будет лежать ниже предыдущей асимптоты на всех достаточна высоких частотах).

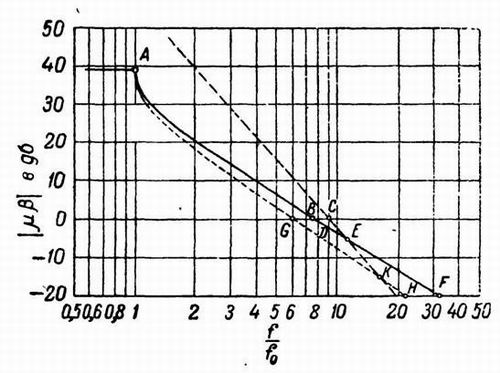
Фиг. 345

На фиг. 345 приведены кривые для системы с обратной связью. Кривая ABEF является воспроизведением характеристики идеального среза, которая уже приводилась на фиг.344. Напомним еще раз, что кривая была построена для значения у = 1/6, что соответствует запасу по величине фазового сдвига в 30° при почти постоянном наклоне, равном 10 дБ на октаву для той части характеристики, которая обозначена через DEF.

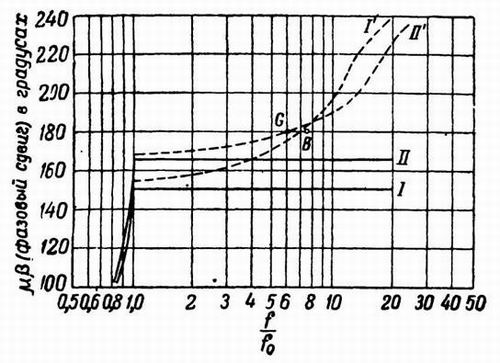
Фиг. 346

Прямая СЕК соответствует асимптоте того типа, который только что рассматривался, при наклоне в 18 дБ на октаву и при величине усиления, равной нулю на частоте ω = 9 ω₀. Так как асимптотические характеристики служат для обозначения практического предела усиления в области верхних частот, то влияние паразитных элементов можно учесть, заменяя теоретическую характеристику среза ломаной линией ABDEK. Угол на кривой в точке Е для действительной схемы был бы, разумеется, сглажен, однако это обстоятельство не может оказать сколько-нибудь заметного влияния на количественный результат. Ввиду того что линии EF и ЕК расходятся между собой на 8 дБ на октаву, влияние паразитных элементов можно изучить путем добавления кривой того типа, которая была приведена на фиг. 220 к исходной характеристике среза. Фазовая характеристика для идеального случая представлена в виде кривой I фиг. 346. Если учесть дополнительный фазовый сдвиг, соответствующий наклону амплитудно-частотной характеристики в области высоких частот в 8 дБ на октаву, то мы получим результирующую фазочастотную характеристику, приведенную в виде кривой I. В точке В, где |μβ| = 1, дополнительный сдвиг по фазе составляет 35°. Так как эта величина больше, чем величина исходного запаса по фазовому сдвигу, которая равнялась 30°, то усилитель при наличии паразитных элементов будет неустойчив. В данном случае устойчивость может быть достигнута, если уменьшить у до 1/12, что будет соответствовать линии AGKH фиг. 345. При этом величина запаса по фазовому сдвигу уменьшается до 15°, однако частотный интервал между О и К настолько шире интервала между В и Е, что величина дополнительного сдвига уменьшается еще сильнее и оказывается меньше 15° в новой точке G. Это показано с помощью кривых II и II ' на фиг. 346. С другой стороны, если линия нулевого усиления будет пересекать асимптоту СЕК в области несколько более низких частот, то никакие изменения одной величины у не окажутся достаточными. Чтобы обеспечить устойчивость работы, здесь уже придется уменьшить степень обратной связи в пределах всей рабочей полосы.

Часть [1]  [2]  [3]  [4]  [5]  [6]  [7]  [8]  [9]  [10]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

Услуга от компании Наша Белка - уборка квартир не оставит вас равнодушным!

Рекомендуем: виртуальную юридическую консультацию

Неповторимый дизайн catalano из Италии

Маркетинговые исследования музыкального и других рынков

Это интересно

В последующих разделах рассмотрение вопроса о влиянии асимптотических характеристик на ограничение допустимой величины обратной связи будет основываться на соотношениях несколько более общих, чем соотношения между характеристикой идеального среза и асимптотой, определяемые кривыми фиг. 345 и 346. Но даже то упрощенное представление, которое может быть получено на основании изучения этих фигур, оказываемся достаточным для выяснения важной роли, какую асимптотические характеристики играют в вопросах проектирования. Очевидно, что большую величину обратной связи не удается получить в том случае, когда асимптота пересекает линию нулевого усиления слишком близко к области рабочего диапазона или же тогда, когда асимптота имеет слишком большую крутизну.
    К счастью, асимптотические характеристики могут быть относительно легко построены, так как они зависят только от паразитных параметров и, может быть, еще от некоторых других элементов схемы. Таким образом, эту характеристику можно вычислить с помощью упрощения действительной схемы. Во избежание напрасной потери времени, которую могло бы повлечь за собой выполнение практически неосуществимого варианта обратной связи, подобный расчет асимптоты желательно сделать как можно раньше, во всяком случае до того, как сделан подробный расчет усилителя.
    Вообще говоря, асимптотические характеристики определяются отчасти емкостями ламп и межкаскадных элементов, а отчасти — входной и выходной цепями и самой β-цепью. Подобное разделение, естественно, возникает в связи с рассмотрением вопроса о схеме фиг. 343. Приведенная там схема относится к предельному случаю, для которого влияние входной, выходной и β-цепи на асимптотическую характеристику снижено до нуля благодаря упрощению схемы усилителя в целом. Задача, стоящая перед инженером при проектировании, значительно шире, чем та, которая связана с созданием схемы, имеющей заданную асимптотическую характеристику. Общее решение, которое будет получено, отчасти зависит от вида обратной связи, а отчасти от того, каким образом разрешается вопрос о получении достаточно сильной обратной связи при соответствующих значениях прочих параметров, усилителя.
    Указанные соображения удобнее всего пояснить, возвращаясь к вопросу об асимптотических характеристиках, который мы разберем для случая простых схем, уже рассмотренных ранее. Если мы начнем с усилителей с обратной связью по напряжению, то в качестве типичной схемы можно выбрать схему фиг. 344.
    На фиг. 347 показана соответствующая предельному случаю асимптотическая цепь перехода от анода последнего каскада к сетке первого каскада. Наличие входных и выходных трансформаторов в схеме можно учесть добавлением параллельно конденсаторам C1 и С4 емкостей, эквивалентных распределенным емкостям обмоток. Чтобы схема обладала наибольшей эффективностью, эти дополнительные емкости должны быть невелики. Если мы будем, однако, стремиться сделать их слишком малыми, например, за счет уменьшения числа витков обмоток, то можем ухудшить другие параметры схемы.
    В нашей "асимптотической" схеме β-цепь представлена последовательно включенными емкостями С5 и С6. Для получения максимальной обратной связи величина этих емкостей должна быть взята значительной. В сущности говоря, их емкость может быть взята сколь угодно большой, так как при любой величине потерь в β-цепи, уменьшая величину сопротивления в токовой цепи обратной связи Т-образной схемы фиг. 344, мы получим также уменьшение на соответствующую величину сопротивления цепи, относящейся к обратной связи по напряжению. Однако, если величина сопротивления β-цепи будет сделана очень малой, то в пределах рабочей полосы может проявлять себя ее шунтирующее влияние на входную и выходную цепи усилителя.
    Далее...