|
Пространственное звучание.
Человек слышит двумя ушами и за счет этого способен различать направление прихода звуковых сигналов. Эту способность
слуховой системы человека называют бинауральным эффектом. Механизм распознавания направления прихода звуков
сложен и, надо сказать, что в его изучении и способах применения еще не поставлена точка.
Уши человека расставлены на некотором расстоянии по ширине головы. Скорость распространения звуковой волны относительно
невелика. Сигнал, приходящий от источника звука, находящегося напротив слушателя, приходит в оба уха одновременно, и мозг
интерпретирует это как расположение источника сигнала либо позади, либо спереди, но не сбоку. Если же сигнал приходит от
источника, смещенного относительно центра головы, то звук приходит в одно ухо быстрее, чем во второе, что позволяет мозгу
соответствующим образом интерпретировать это как приход сигнала слева или справа и даже приблизительно определить угол прихода.
Численно, разница во времени прихода сигнала в левое и правое ухо, составляющая от 0 до 1 мс, смещает мнимый источник звука
в сторону того уха, которое воспринимает сигнал раньше. Такой способ определения направления прихода звука используется мозгом
в полосе частот от 300 Гц до 1 кГц. Направление прихода звука для частот расположенных выше 1 кГц определяется мозгом человека
путем анализа громкости звука. Дело в том, что звуковые волны с частотой выше 1 кГц быстро затухают в воздушном пространстве.
Поэтому интенсивность звуковых волн, доходящих до левого и правого ушей слушателя, отличаются на столько, что позволяет мозгу
определять направление прихода сигнала по разнице амплитуд. Если звук в одном ухе слышен лучше, чем в другом, следовательно
источник звука находится со стороны того уха, в котором он слышен лучше. Немаловажным подспорьем в определении направления
прихода звука является способность человека повернуть голову в сторону кажущегося источника звука, чтобы проверить верность
определения. Способность мозга определять направление прихода звука по разнице во времени прихода сигнала в левое и правое
ухо, а также путем анализа громкости сигнала используется в стереофонии.
Имея всего два источника звука можно создать у слушателя ощущение наличия мнимого источника звука между двумя физическими.
Причем этот мнимый источник звука можно «расположить» в любой точке на линии, соединяющей два физических источника. Для этого
нужно воспроизвести одну аудио запись (например, со звуком рояля) через оба физических источника, но сделать это с некоторой
временной задержкой в одном из них и соответствующей разницей в громкости. Грамотно используя описанный эффект можно
при помощи двухканальной аудио записи донести до слушателя почти такую картину звучания, какую он ощутил бы сам, если бы
лично присутствовал, например, на каком-нибудь концерте. Такую двухканальную запись называют стереофонической. Одноканальная
же запись называется монофонической.
На самом деле, для качественного донесения до слушателя реалистичного пространственного звучания обычной стереофонической
записи оказывается не всегда достаточно. Основная причина этого кроется в том, что стерео сигнал, приходящий к слушателю
от двух физических источников звука, определяет расположение мнимых источников лишь в той плоскости, в которой расположены
реальные физические источники звука. Естественно, «окружить слушателя звуком» при этом не удается. По большому счету по той
же причине заблуждением является и мысль о том, что объемное звучание обеспечивается квадрофонической (четырехканальной)
системой (два источника перед слушателем и два позади него). В целом, путем выполнения многоканальной записи нам удается
лишь донести до слушателя тот звук, каким он был «услышан» расставленной нами звукопринимающей аппаратурой (микрофонами),
и не более того. Для воссоздания же более или менее реалистичного, действительно объемного звучания прибегают к применению
принципиально других подходов, в основе которых лежат более сложные приемы, моделирующие особенности слуховой системы человека,
а также физические особенности и эффекты передачи звуковых сигналов в пространстве.
Одним из таких инструментов является использование функций HRTF (Head Related Transfer Function). Посредством этого метода
(по сути – библиотеки функций) звуковой сигнал можно преобразовать специальным образом и обеспечить достаточно реалистичное
объемное звучание, рассчитанное на прослушивание даже в наушниках.
Суть HRTF – накопление библиотеки функций, описывающих психофизическую модель восприятия объемности звучания слуховой
системой человека. Для создания библиотек HRTF используется искусственный манекен KEMAR (Knowles Electronics Manikin for
Auditory Research) или специальное «цифровое ухо». В случае использования манекена суть проводимых измерений состоит в следующем.
В уши манекена встраиваются микрофоны, с помощью которых осуществляется запись. Звук воспроизводится источниками, расположенными
вокруг манекена. В результате, запись от каждого микрофона представляет собой звук, «прослушанный» соответствующим ухом манекена
с учетом всех изменений, которые звук претерпел на пути к уху ( затухания и искажения как следствия огибания головы и отражения
от разных ее частей). Расчет функций HRTF производится с учетом исходного звука и звука, «услышанного» манекеном. Собственно,
сами опыты заключаются в воспроизведении разных тестовых и реальных звуковых сигналов, их записи с помощью манекена и дальнейшего
анализа. Накопленная таким образом база функций позволяет затем обрабатывать любой звук так, что при его воспроизведении
через наушники у слушателя создается впечатление, будто звук исходит не из наушников, а откуда-то из окружающего его пространства.
Таким образом, HRTF представляет собой набор трансформаций, которые претерпевает звуковой сигнал на пути от источника
звука к слуховой системе человека. Рассчитанные однажды опытным путем, HRTF могут быть применены для обработки звуковых сигналов
с целью имитации реальных изменений звука на его пути от источника к слушателю. Не смотря на удачность идеи, HRTF имеет,
конечно, и свои отрицательные стороны, однако в целом идея использования HRTF является вполне удачной. Использование HRTF
в том или ином виде лежит в основе множества современных технологий пространственного звучания, таких как технологии QSound
3 D ( Q3 D), EAX, Aureal3 D ( A3 D) и другие.
Цифровые аудио сигналы
Компьютер – это цифровое устройство, то есть электронное устройство, в котором рабочим сигналом является дискретный сигнал.
Сегодняшние компьютеры оперируют дискретными сигналами, несущими двоичные значения, условно обозначаемые как «да» и «нет»
(на электрическом уровне: 0 вольт и V вольт, для некоторого ненулевого значения V). С помощью одного двоичного сигнала за
один шаг можно передать информацию об одном из всего двух положений: 0 («да») или 1 («нет»). С помощью N двоичных сигналов
за один шаг можно передать информацию об одном из 2 N положений (2 N – это число комбинаций нулей и единиц для N сигналов).
Взаимодействие всех составляющих компьютер блоков происходит путем обмена и обработки одним или одновременно несколькими
двоичными сигналами. Все – коды управления, а также сама обрабатываемая информация – все представляется в компьютере в виде
чисел. По этой причине и аудио сигналы в цифровой аппаратуре представляют в виде чисел.
Итак, каким же образом можно описать аналоговый аудио сигнал в цифровой форме? Реальный аудио сигнал – это сложное по
форме колебание, некая сложная зависимость амплитуды звуковой волны от времени. Преобразование аналогового звукового сигнала
в цифровой вид называется аналогово-цифровым преобразованием или оцифровкой. Процесс такого
преобразования заключается в:
· осуществлении замеров величины амплитуды аналогового сигнала с некоторым
временным шагом - дискретизация;
· последующей записи полученных значений амплитуды в численном виде – квантование.
Дискретизация
Процесс дискретизации по времени - это процесс получения мгновенных значений преобразуемого аналогового
сигнала с определенным временным шагом, называемым шагом дискретизации (см. рис. 7).
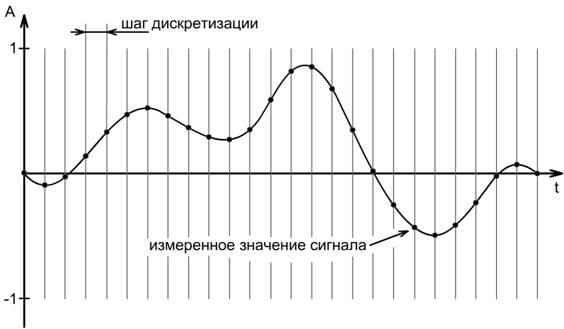
Количество осуществляемых в одну секунду замеров величины сигнала называют частотой дискретизации или
частотой выборки, или частотой сэмплирования (от англ. « sampling» – «выборка»).
Очевидно, что чем меньше шаг дискретизации, тем выше частота дискретизации (то есть, тем чаще регистрируются значения
амплитуды), и, значит, тем более точное представление о сигнале мы получаем. Это рассуждение подтверждается доказанной теоремой,
теоремой Котельникова (в зарубежной литературе встречается как теорема Шеннона, Shannon). Согласно этой
теореме, аналоговый сигнал с ограниченным спектром может быть точно описан дискретной последовательностью значений его амплитуды,
если эти значения следуют с частотой, как минимум вдвое превышающей наивысшую частоту спектра. Иначе говоря, аналоговый сигнал,
в котором частота наивысшей составляющей спектра равна F m, может быть точно описан последовательностью дискретных значений
амплитуды, если для частоты дискретизации F d выполняется: 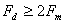 . На практике это
означает следующее: для того, чтобы оцифрованный сигнал содержал информацию о всем диапазоне слышимых человеком частот исходного
аналогового сигнала (0 – 20 кГц) необходимо, чтобы выбранное значение частоты дискретизации при оцифровке сигнала составляло
не менее 40 кГц.
Казалось бы, для завершения процесса оцифровки теперь осталось лишь записать измеренные мгновенные значения амплитуды
сигнала в численной форме. Полученная последовательность чисел (по одному результату замера амплитуды сигнала на каждый шаг)
и образует цифровую форму исходного аналогового сигнала – так называемый импульсный сигнал . Здесь, однако,
обнаруживается основная трудность оцифровки, заключающаяся в невозможности записать измеренные значения сигнала с идеальной
точностью.
Линейное (однородное) квантование
Допустим, что для записи одного значения амплитуды сигнала в памяти компьютера мы отводим N бит. Соответственно, с помощью
одного N -битного слова (слово – последовательность N бит) можно описать 2 N разных положений. Допустим
теперь, что амплитуда оцифровываемого сигнала колеблется в пределах от -1 до 1 некоторых условных единиц. Заметим, что измеренным
значениям амплитуды ничто не мешает быть дробными (например, -0.126 или 0.997). Представим этот диапазон изменения амплитуды
- динамический диапазон сигнала - в виде 2 N -1 равных промежутков, разделив его на 2 N уровней
- квантов (произведя таким образом однородное, линейное разбиение амплитудной шкалы). Теперь, для записи
каждого отдельного значения амплитуды, его необходимо округлить до ближайшего уровня квантования. Этот процесс называется
квантованием по амплитуде. Говоря более формальным языком, квантование по амплитуде – это процесс замены
реальных (измеренных) значений амплитуды сигнала значениями, приближенными с некоторой точностью. Каждый из 2 N возможных
уровней называется уровнем квантования,а расстояние между двумя ближайшими уровнями квантования называется
шагом квантования. В случае линейного разбиения амплитудной шкалы на уровни, квантование называют линейным
(однородным) . На рис. 8 представлен пример такого квантования.
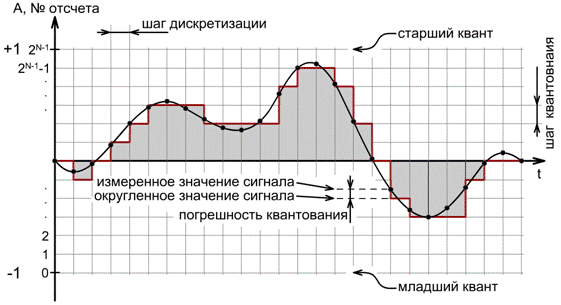
Как видно, результатом такой оцифровки стал ступенчатый сигнал, составленный из прямоугольников, каждый из которых имеет
ширину равную величине шага дискретизации, и высоту равную измеренному значению амплитуды сигнала.
Очевидно, что точность округления зависит от выбранного количества (2 N) уровней квантования, которое, в свою очередь,
зависит от количества бит ( N), отведенных для записи значения амплитуды. Чем больше уровней квантования и чем ближе они
друг к другу (а, для некоторого фиксированного диапазона изменения амплитуды расстояние между уровнями квантования обратно
пропорционально их количеству), тем на меньшую величину приходится округлять измеренные значения амплитуды, и, таким образом,
тем меньше получаемая погрешность квантования. Число N называют разрядностью квантования
(подразумевая количество разрядов, то есть бит, в каждом слове), а полученные в результате округления значений амплитуды
числа – отсчетами или сэмплами (от англ. “ sample” – “замер”).Считается, что погрешность
квантования, являющаяся результатом квантования с разрядностью 16 бит, остаются для слушателя почти незаметными.
Описанный способ оцифровки сигнала - дискретизация сигнала во времени в совокупности с методом однородного квантования
- называется импульсно-кодовой модуляцией, ИКМ (англ. Pulse Code Modulation – PCM).
Стандартный аудио компакт-диск ( CD- DA), применяющийся с начала 80-х годов 20-го столетия, хранит информацию в формате PCM,
с частотой дискретизации 44.1 кГц и разрядностью квантования 16 бит.
Часть [1]
[2]
[3]
[4]
[5]
[6]
|
