Это интересно

Современному инженеру в практической деятельности приходится иметь дело с проектированием и эксплуатацией студий звукозаписи, звукового и телевизионного вещания, систем и устройств звукоусиления в производственных помещениях, аудиториях, театральных и концертных задах. В связи с этим ему необходимо знать и понимать основные положения акустики помещений (строительной, архитектурной акустики) и применять эти положения при решении возникающих задач.
    Цель статьи - ознакомить с историей, развитием и сов-ременным состоянием этой важной отрасли акустики как науки, дать некоторые знания, которые могут понадобиться при выполнении проектов, частью которых является акустический расчет перечисленных объектов.
    Истоки архитектурной  (строительной) акустики восходят к глубокой древности. Акустические задачи в те времена ставились и решались в связи со строительством гигантских сначала культовых, а позже и других общественных сооружений - залов для собраний и зрелищ.
    Зодчие Ассирии, Вавилона, Древнего Египта в V-II тысячелетиях до н. э. строили храмы, обладавшие выразительной архитектурой и впечатляющим художественным убранством. И мощные строительные конструкции, и скульптура, и живопись - все было направлено на то, чтобы поразить и подавить психику молящихся, создать у них ощущение своего ничтожества, мистического страха перед божественными силами. Зодчим, по-видимому, уже были известны законы распространения и отражения звуковых волн. Пользуясь ими, они достигали акустических эффектов, поражавших воображение молящихся.
    Иные, хотя и столь же сильные чувства возбуждало искусство Древней Греции (VII-IV вв. до н. э.) - одной из вершин мировой цивилизации. В отличие от искусства Древнего Египта в основе древнегреческого лежало представление о силе и красоте человека, его неразрывной связи с окружающей природой и общественной средой. Искусство Древней Греции отличалось гармоничностью и светлыми чувствами.
    Древним греческим храмам и другим общественным сооружениям свойственна соразмерность частей, она определила их высокие акустические свойства. Рациональность принятых древними греками акустических решений была впоследствии подтверждена наукой нашего времени.
    Наряду с храмовыми зданиями уделялось большое внимание сооружениям общественного назначения. Зрелищные сооружения Древней Греции разделялись на два вида: одейоны и театры. Первые представляли собой сравнительно небольшие крытые здания для репетиций и представлений с малым количеством исполнителей (без хора) и зрителей, вторые являлись зрелищными сооружениями открытого типа и большой вместимости (тысячи и десятки тысяч человек). Каменные скамьи зрительских мест располагались на склонах возвышенностей.
    Традиции греческих архитекторов были продолжены их римскими последователя в VII-I вв. до нашей эры. Римские театры на открытом воздухе были сходны с греческими, хотя в отличие от них строились не только на естественных склонах, но и на горизонтальных участках. Типичным примером такого театра служит амфитеатр Флавия - Колизей на 56 тыс. зрителей, построенный в 80-90 гг. н. э.
    В наше время требуется установка систем звукоусиления даже в залах вместимостью 200-300 человек. Поэтому кажутся фантастическими свидетельства историков о вместимости древних греческих и римских театров, обслуживающихся естественной звучностью голосов актеров. Так, театр Помпея вмещал 17800 человек, театр Марцелла в Риме - 20 тыс. человек. Если даже эти данные сильно преувеличены (по современным оценкам, названные театры вмещали соответственно 5 и 7 тыс. человек), то кажется чудом, что в этих гигантских театрах достигали удовлетворительной звучности на слушательских местах. Остается предположить: либо уши тогдашних посетителей зрелищ были в несколько раз чувствительнее современных, либо древние строители знали неведомые нам секреты, позволявшие получить достаточную громкость и разборчивость на слушательских местах. Известно, что в маски актеров, изображающие различные эмоции действующих лиц, были встроены рупоры, направлявшие звук в сторону зрителей...
    Далее...

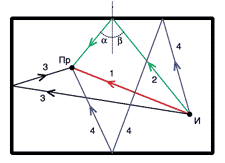
Рис. 2. Прямой и отраженные сигналы

Рассмотрим процессы, происходящие в помещении при звучании источника И (рис. 2). Первым в точку приема Пр, где находятся уши слушателя или микрофон, приходит по пути 1 прямой звук, затем по пути 2 звуки, отраженные от ближайших к источнику поверхностей, далее звуки по пути 3, отраженные от удаленных поверхностей. Позже приходят звуки, претерпевшие двукратные отражения на пути 4, и т. д. Количество отражений в единицу времени возрастает пропорционально второй степени времени. Помещение постепенно заполняется звуковой энергией. После прекращения звучания источника начинается процесс отзвука. В той же последовательности, как и при начале звучания, сперва в точку приема приходят сравнительно редкие начальные отражения. 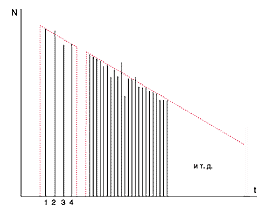Далее плотность запаздывающих импульсов увеличивается, а их энергия постепенно спадает (рис. 3).

Рис. 3. Структура ранних отражений реверберационного отклика

Статистическая теория занимается именно этой, второй частью отзвука с повышающейся плотностью импульсов во времени и уменьшающейся их энергией. Прямой звук и начальные сравнительно редкие отражения статистической теорией не принимаются во внимание.

Метод, предложенный У. Сэбином, основан на модели идеального помещения, в котором звуковое поле после прекращения действия звукового сигнала может быть рассчитано на основе статистического рассмотрения процесса затухания звука. При этом предполагается, что амплитуды и фазы отраженных звуковых волн распределены хаотически, т. е. в волновом движении нет преобладающих направлений потоков и симметрии в распределении амплитуд. Принятое допущение позволяет считать, что средние значения звуковой энергии по различным направлениям одинаковы, т. е. звуковое поле изотропно, и средняя по времени плотность звуковой энергии в любой точке помещения тоже одинакова. Такое звуковое поле называют диффузным. Его рассмотрение дало возможность пренебречь явлениями интерференции и применить при расчетах энергетическое суммирование. Этот подход подобен используемому в кинетической теории газов и основан на математической теории вероятностей. Л. Бреховских показал, что для помещений, линейные размеры которых велики по сравнению с длиной волны, получаются достаточно удовлетворительные результаты.

Методами математической статистики в диффузном поле определяют среднюю длину пробега звукового луча между двумя отражениями. Для помещения в форме прямоугольного параллелепипеда с линейными размерами, близкими к "золотому сечению" (длина относится к ширине и к высоте, как 2 : 2^0,5 : 1, по другому определению 5 : 3 : 2), статистически определенная средняя длина свободного пробега звукового луча

lср = 4V / S ,

где V - объем помещения, S - общая площадь всех ограничивающих поверхностей (пола, потолка, стен).

Впоследствии было установлено, что полученная зависимость примерно сохраняется и для помещений, линейные размеры которых отклоняются от "золотого сечения", и для помещений более сложной формы.

При каждом отражении часть падающей энергии поглощается преградами и превращается в тепло. Процесс постепенного уменьшения плотности звуковой энергии У. Сэбин назвал реверберацией (reverberation в переводе означает "отражение", "отзвук"). В Германии для обозначения этого процесса используется слово Nachhall, в переводе на русский "отзвук", "отголосок", "отклик". Термин "отзвук" ранее встречался и в русской технической литературе.

За длительность процесса, реверберации - время реверберации - было принято считать промежуток, за который плотность звуковой энергии уменьшается в 106 раз, звуковое давление в 103, а уровень звукового давления на 60 дБ.

Прямых объяснений мотивов выбора спада уровня на 60 дБ нет. Попытаемся найти разумные причины. Фортиссимо оркестра соответствуют уровни звукового давления 90-100 дБ, а пианиссимо - 35-40 дБ. Тогда средние уровни составят 63-70 дБ и принятое по определению (спад на 60 дБ) время реверберации будет примерно соответствовать длительности спада средних уровней до порога слышимости. Возможно, данное обстоятельство и стало причиной выбора такого определения времени реверберации.

Разумеется, все это справедливо в отсутствии акустических помех. При шумах, например, с уровнями 30-40 дБ, что характерно и для жилой комнаты, и для концертного зала, значительная часть отзвука будет маскироваться шумами, и слышимый отзвук будет длиться менее половины времени реверберации.

Расчетные соотношения. Для экспериментального определения времени реверберации Сэбин пользовался простейшими приспособлениями: органными трубами как источником звука и секундомером. Он нашел, что время реверберации Т прямо пропорционально объему помещения V и обратно пропорционально произведению среднего коэффициента поглощения aср и площади всех преград S:

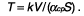
Средний коэффициент поглощения:

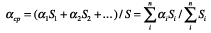
где a1, a2,... - коэффициенты поглощения различных материалов;

S = S1 + S2 + ... - общая площадь преград; n - количество разных преград.

Из этого выражения можно заключить, что средний коэффициент поглощения соответствует единому материалу, которым можно было бы покрыть все поверхности преград помещения с сохранением общего звукопоглощения А = aсрS. Единицей поглощения считают 1 м2 открытого проема, полностью поглощающего всю падающую на него энергию (без учета дифракции). Эту единицу назвали сэбин (Сб).

По измерениям времени реверберации в пяти различных помещениях в форме прямоугольного параллелепипеда и объемами от 96 до 1960 м3 У. Сэбин принял значение коэффициента k = 0,164 (это число примерно равно хорошо запоминающейся дроби 1/6). При теоретическом выводе формулы для расчета времени реверберации было получено значение k = 0,161, которое и указывается в большинстве учебников. Чтобы согласовать физические размерности в левой и правой частях формулы, было решено придать коэффициенту k размерность с/м.

В дальнейшем было обнаружено, что k различно для помещений разной формы. Измеренные значения k приведены в таблице.

Из приведенных примеров видно, что форма помещения влияет на значение времени реверберации, хотя из структуры самой формулы У. Сэбина это не вытекает. Дело в том, что от соотношения линейных размеров зависит средняя длина пробега между двумя отражениями lcр, следовательно, зависит и время реверберации Т.

Теоретический вывод формулы Сэбина основан на предположении о диффузном, равномерном распределении звуковой энергии по пространству помещения и о непрерывном поглощении энергии преградами в процессе реверберации.

Это допущение дает сравнительно небольшое отклонение рассчитанной величины Т от измеренной, если средний коэффициент поглощения мал, и поэтому количество отражений получается достаточно большим, чтобы пренебречь дискретностью этого процесса.

На самом деле звуковая энергия поглощается преградами не непрерывно, а скачками, по мере достижения волной той или иной поверхности. Поэтому вполне равномерного заполнения энергией всего объема по-мещения не будет.

Более точные исследования реверберации были проведены в 1929 г. Шустером и Ветцманом, а в 1930 г. - Карлом Эйрингом. Формула Эйринга имеет вид:

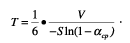
Разложив выражение ln(1-a) в ряд и оставив в нем ввиду малости a только первый член, обнаружим, что при небольших значениях a формула Эйринга переходит в формулу Сэбина. Действительно,

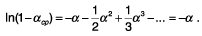
Объясним смысл знака минус в знаменателе формулы. Логарифм чисел меньше единицы имеет отрицательное значение. Знак минус введен, чтобы исключить физическую несообразность - отрицательное значение Т. Выражение, стоящее в знаменателе, является эквивалентом общего поглощения А = aсрS, содержащегося в формуле Сэбина.

Сравнивая формулы Сэбина и Эйринга, приходим к выводу, что приближение Сэбина дает завышенное значение T. Расхождение увеличивается с возрастанием aср:

При значении aср = 1 получается физически нереальный результат: T= V/6S, хотя в этом случае должно  Т = 0.

Формулы Сэбина и Эйринга могут быть применены, если звукопоглощающие материалы распределены по ограждающим помещение поверхностям достаточно равномерно, чтобы можно было пользоваться понятием среднего коэффициента поглощения.

Для оптимизации акустических условий в концертных залах рекомендуется aср = 0,19. Поэтому вполне допустимо время реверберации в этом случае рассчитывать по формуле Сэбина.

При выводе формулы Сэбина и Эйринга приняты некоторые допущения, которые редко оговариваются в литературе по акустике. Формула Сэбина получена в предположении, что волны падают на преграды под любыми углами, а при выводе формулы Эйринга принято, что волны падают на преграды под углами, близкими к нормали. Поэтому, строго говоря, в формулу Сэбина следовало бы подставлять значения коэффициента поглощения, определенные в диффузном поле, в реверберационной камере, а в формулу Эйринга - значения коэффициента поглощения, измеренные в плоском поле, при нормальном падении, т. е. в трубе.

При очень неравномерном распределении общего поглощения результат, вычисленный по формуле Эйринга, может оказаться далеким от измеренного. Миллингтон (Millington) объяснил причину этого расхожде-ния. Эйринг полагал, что число отражений от разных поверхностей с площадями S1, S2,... одинаково. В действительности вероятность числа отражений от данной поверхности тем больше, чем больше сама поверхность. На основании этих соображений Миллингтон вывел иную формулу для расчета времени реверберации:

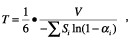
где Si - площадь материалов с коэффициентами поглощения ai.

Недостаток формулы Миллингтона заключается в следующем: вычисленное значение времени реверберации получается равным нулю, если хотя бы один элемент преграды, как бы он ни был мал, имеет aср  = 1. По-видимому, при выводе формулы было принято какоето сомнительное допущение. Впрочем, парадоксального результата легко избежать, приняв, что ни один коэффициент поглощения не равен единице.

Практика показала, что для помещений с небольшим aср (театральные и концертные залы, учебные аудитории и т. п.) все три формулы дают одинаково удовлетворительный результат. Для помещений со средними коэффициентами затухания (например, студии) более близки к измеренным значения времени реверберации, рассчитанные по формуле Эйринга. Если материалы имеют сильно различающиеся ai, а сами материалы распределены по поверхностям неравномерно, более близкими к измеренным получаются значения Т, рассчитанные по формуле Миллингтона. Используя названные формулы, необходимо принять те a, которые были рассчитаны с помощью этих же формул при обработке экспериментального материала, полученного в звукомерной камере.

Определение коэффициента поглощения.   Коэффициенты поглощения материалов определяют измерениями в "гулкой" (реверберационной) камере. Обозначим объем камеры через V, а ее время реверберации через TO. После внесения в камеру исследуемого материала с площадью SM время реверберации уменьшается до TM. Тогда:

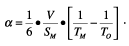
Если площадь исследуемого предмета (например, стола, кресла и т. д.) не может быть выражена определенным числом, находят поглощение предмета

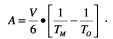
Итак, с помощью вышеприведенных формул Сэбина и Эйринга решают обратную задачу: определяют a или А по измеренному времени реверберации.

А. П. Ефимов, профессор МТУСИ

Опубликовано по материалам http://www.install-pro.ru/archive/005/44-49.shtml

Часть [1]  [2]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Это интересно

Многие годы производители транзисторных усилителей водили аудиофилов за нос, предлагая им правдоподобные объяснения, почему следует старую модель усилителя заменить на новую. Коротко напоминаю эти объяснения:
    - слишком велики гармонические искажения (в новых моделях усилителей искажения снижены до 0,0001%);
    - мал коэффициент демпфирования (коэффициент демпфирования достиг 1000);
    - недостаточно широка полоса воспроизводимых частот (полоса была расширена до 5 МГц);
    - усилители ограничивают скорость изменения сигнала (на лицевых панелях новых усилителей появилась надпись High Speed Amplifier");
    - громкоговоритель требует большего тока (и вот множество включенных параллельно выходных транзисторов обеспечивают выходной ток усилителя 100 А).
    Этот список можно было бы продолжить.
    Пока удавалось поддерживать у адиофилов веру во все эти технические "заморочки", на рынке усилителей царило оживление...
    Имеет ли лампа преимущество перед транзистором? И если имеет, то при каких условиях они проявляются? Ответы Вы найдете в этой статье.
    Чтобы сразу не впасть в мистику, рассмотрим на физическом уровне различия между лампой, полевым и биполярным транзисторами.
    Лампу (возьмем в качестве примера триод) можно рассматривать как "проводник", который состоит из тщательно очищенных от кислорода электродов - анода и катода, - а также вакуумного промежутка между ними, заполненного носителями заряда - энергетически возбужденными свободными электронами. Переносимый через вакуум свободными электронами ток анода управляется напряжением между сеткой и катодом.
    Усилительные свойства триода можно характеризовать крутизной характеристики, то есть отношением приращения тока анода к приращению напряжения "сетка - катод" (при неизменном напряжении на аноде). Независимость крутизны от электрических режимов лампы является показателем ее линейности. Особенно важно, что крутизна характеристики триода мало зависит от тока анода (в большинстве случаев она пропорциональна примерно корню 3-й степени из величины этого тока). Влиянием входной характеристики лампы ва линейность можно пренебречь, так как в режиме отрицательного смещения сетки ток в ее цепи отсутствует.
    Межэлектродные емкости постоянны и не зависят от электрических ре-жимов лампы. Немаловажно также то, что основные параметры лампы не зависят от температуры анода или, иначе, от выделяемой на нем мощности. И еще одно важное преимущество именно триода - низкое внутреннее сопротивление, которое при оптимальном режиме использования лампы меньше сопротивления нагрузки приблизительно в два раза.
    Зависимость внутреннего сопротивления от тока анода обратна зависимости крутизны триода от этого тока, поэтому в режиме, а котором сопротивление нагрузки больше внутреннего сопротивлений, усиление лампы практически не зависит от тока анода.
    Полевой транзистор тоже можно рассматривать как "проводник". Проводящей частью транзистора является канал в кристалле сверхчистого кремния, тип проводимости которого (p или n) задается ничтожной примесью индия или мышьяка. В зависимости от типа проводимости транзистора а канале перемещаются носители заряда: свободные электроны или "дырки" (не заполненные электронами места в кристаллической решетке). Как и в ламповом триоде, ток на выходе полевого транзистора (ток стока) управляется напряжением между затвором и истоком.
    Усилительные свойства полевого транзистора (как и лампы) можно характеризовать крутизной (то есть отношением приращения тока стока к приращению напряжения "затвор - исток").
    Полевой транзистор имеет более выраженную нелинейность, чем лампа. Почти у всех типов полевых транзисторов крутизна увеличивается пропорционально квадратному корню из величины тока стока...
    Далее...