Это интересно

Звук передается колебаниями частиц воздуха. Чтобы частицы воздуха могли совершить звуковые колебания, необходимо, чтобы они каким-то образом были приведены в колебательное состояние или, как принято говорить в акустике, были «возбуждены». Таким возбудителем или, иначе говоря, источником звука может быть, например, диффузор громкоговорителя, струна скрипки и т. н. Здесь колебания твердых тел (диффузор, струна) вызывают колебания частиц воздуха.
    Твердое тело или совокупность нескольких твердых тел, участвующих в колебаниях, называется механической колебательной системой. Движение этих тел характеризуется либо перемещением к какой-нибудь точки тела, либо скоростью этой точки х, либо с ускорением х′.
    Рассмотрим простую механическую колебательную систему (рис. 1), состоящую из массы т, укрепленной на пружине имеющей упругость s. Масса находится в вязкой среде, создающей сопротивление трения r. Если конец пружины оттянут из положения равновесия на расстояние х, то пружина стремится сократиться с некоторой силой. Очевидно, что эта сила тем больше, чем на большее расстояние оттянута пружина и чем больше ее упругость. Отсюда возвращающая сила пружины Fs, стремящаяся вернуть оттянутый ее конец в положение равновесия, равна произведению xs, где х — расстояние, на которое оттянут конец пружины, a s — коэффициент упругости пружины.
    В свою очередь s определяется как s=F s / x.
    Отсюда единицей упругости называется упругость такой пружины, которая при растяжении на единицу длины (1 м) стремится сократиться с силой, равной также единице (1 Н).
    Свойства пружины можно характеризовать и величиной, обратной коэффициенту упругости. Эта величина называется коэффициентом гибкости и обозначается буквой с: c=1/s и соответственно c=x/Fs.
    При перемещении тела возникают силы трения, тормозящие движение тела. При движении тела в вязкой среде значение силы трения Fr пропорционально скорости тела х и коэффициенту r, характеризующему среду, в которой возникает трение, и называемому обычно сопротивлением трения. Следует заметить, что сопротивление трения может возникать не только при движении тела в вязкой среде, но и в результате внутреннего трения, например, трения частиц в толще материала пружины при ее растяжении или сжатии.
    Сопротивление трения — одна из составляющих активного механического сопротивления. Характерной особенностью реальной механической системы (обладающей активным механическим сопротивлением) является то, что в ней всегда имеет место необратимый переход механической энергии в тепловую.
    Сила трения может быть выражена как Fr=rx или r=Fr/x.
    Единицей активного сопротивления (трения) называется такое сопротивление, которое при перемещении тела со скоростью, равной единице (1 м/с), вызывает тормозящую силу, равную также единице (1 Н). Единица активного сопротивления измеряется в кГ/с (если учесть размерность силы кГ·м/с2).
    Все тела стремятся сохранить состояние покоя или равномерного прямолинейного движения. Изменению этого состояния они сопротивляются с силой инерции, равной произведению массы на ускорение.
    Пусть к телу с массой т (см. рис. 1) приложена сила F, направленная вниз. Под влиянием этой силы тело опустится на расстояние х от положения равновесия. При этом, кроме внешней силы F, на тело массой т действуют следующие силы: во-первых, сила инерции тх, во-вторых, тормозящая сила трения, равная rх, в-третьих, сила упругости пружины sx, которая стремится вернуть тело в положение равновесия. Процесс в такой механической системе подобен процессу в цепи переменного тока, состоящей из последовательного соединения индуктивности L, активного сопротивления R и емкости С.
    Это подобие отражает тот факт, что в обеих системах имеет место превращение энергии из одного вида в другой. Действительно, в механической системе кинетическая энергия движущегося тела превращается в потенциальную энергию растянутой пружины, и обратно. Часть энергии из-за наличия трения переходит в тепло. В электрической цепи энергия магнитного поля, появляющегося при прохождении электрического тока, превращается в энергию электрического поля (заряд конденсатора), и обратно. Часть энергии выделяется на активном сопротивлении в виде тепла. Поэтому масса, сопротивление трения и гибкость аналогичны соответственно индуктивности, активному сопротивлению и электрической емкости. Это подобие не является чисто внешним, формальным, а отображает физическое подобие рассматриваемых величин или, как их называют, параметров. Действительно, индуктивность в цепи препятствует как мгновенному возрастанию тока от нуля до какого-то конечного его значения при включении источника напряжения, так и спаданию тока до нуля сразу же при выключении напряжения. То же относится к массе в механической системе. Инертность тела препятствует мгновенному нарастанию скорости при приложении силы и не дает телу остановиться сразу.
    Как уже отмечалось, часть энергии электрического тока благодаря наличию активного сопротивления превращается в тепло. Также превращается в тепло при наличии трения часть механической энергии. Чем больше гибкость пружины, тем большее смещение она получает при заданном значении силы. Чем больше электрическая емкость, тем больший заряд создается на конденсаторе при заданном приложенном напряжении. Заряд можно рассматривать как аналог смещения, а ток, следовательно, как аналог скорости. Аналогичны также электродвижущая сила и механическая сила, первая является причиной прохождения тока, вторая — движения тела.
    Отсюда по аналогии колебательная скорость тела в простой колебательной системе, на которую действует сила F, меняющаяся по синусоидальному закону с круговой частотой ω, выражается следующим образом:
    является полным механическим сопротивлением, измеряемым в механических Омах (мехомах).
    Подобно реактивному сопротивлению электрической цени [ωL - 1/(ωС)], являющегося разностью индуктивного (ωL и емкостного 1/(ωС) сопротивлении, в механической системе сопротивление [ωm - 1/(ωC)] называется реактивным механическим сопротивлением и является разностью инерционного сопротивления ωm (обусловленного инертностью тела) и упругого сопротивления 1/(ωC) или s/ω. Механическое реактивное сопротивление также измеряется в мегомах.
    В электротехнике и акустике синусоидально изменяющиеся величины (сила, смещение, скорость, ускорение и т. д.) принято измерять в действующих значениях, которые в √2 раз меньше амплитудных. Укажем, что абсолютные значения амплитудных (и соответственно действующих) значений смещения х, скорости х’ и ускорения х’’ связаны между собой соотношениями:
    В дальнейшем, если не будет оговариваться иное, мы будем пользоваться имение действующими значениями этих и других величин.
    Смещение при колебательном движении измеряется в обычных единицах длины (м), колебательная скорость — в обычных единицах скорости (м/с), а ускорение при этом движении — в обычных единицах ускорения (м/с2).
    Далее...

Бытовые акустические системы

ЭЛЕКТРОМЕХАНИЧЕСКИЕ ПРЕОБРАЗОВАТЕЛИ ЭНЕРГИИ И ИХ ВИДЫ

Применяемые в электроакустике аппараты являются преобразователями одного вида энергии в другой. Например, подводимая к зажимам громкоговорителя электрическая энергия частично затрачивается на нагрев проводника и, таким образом, превращается в тепловую, а частично превращается в механическую энергию колебаний подвижной системы громкоговорителя. Для выяснения сущности процесса преобразования одного вида энергии в другой и связи между электрической цепью и механической колебательной системой преобразователя рассмотрим, для примера, наиболее распространенный в электроакустике электродинамический принцип преобразования.

Из электротехники известно, что если поместить в магнитное поле проводник с током, то он начнет двигаться в направлении, определяемом правилом левой руки. Например, пусть проводник имеет форму плоского витка, в котором ток направлен по часовой стрелке, а магнитные силовые линии направлены по радиусам от центра витка. Тогда сила, которая действует на виток, окажется направленной вверх. При перемене направления тока на обратное сила, действующая на виток, также изменит свое направление. Поэтому, если в проводнике будет протекать переменный ток, то проводник будет колебаться. Наоборот, если виток, находящийся в магнитном поле, колеблется под влиянием какой-либо действующей на него силы и перерезает при этом магнитные силовые линии, то в нем будет индуктироваться э. д. с. Если виток замкнуть, то в цепи потечет ток. Рассмотрим несколько подробнее явления, происходящие при электродинамическом способе преобразования.

Если приложить к катушке, состоящей из нескольких витков и находящейся в магнитном поле, переменное напряжение U, то она начинает колебаться под действием возникающих сил. При этом в витках катушки, которая пересекает магнитные силовые линии, индуктируется э. д. с. Направление э. д. с. по правилу Ленца таково, чтобы противодействовать причине, ее вызвавшей, т. е. приложенному напряжению. Значение противо- э. д. с. равно Blx, где В — магнитная индукция, Тл; l — длина проводника кагушки; м; х— скорость движения катушки, м/с. Если обозначить электрическое сопротивление катушки через R, то по закону Ома ток в ней

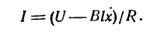(3)

Скорость движения катушки согласно (1) определяется как частное от деления силы F на полное механическое сопротивление z_m. Сила, движущая проводник в магнитном поле, равна, как известно,

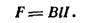(4)

Отсюда x=F/z_m=BlI/z_m.

Подставляя значение скорости х в (3), получаем

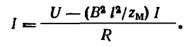(5)

Решая это уравнение относительно I, имеем

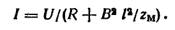(6)

Таким образом, при механических колебаниях катушки с током в магнитном поле в ней возбуждается противо- э. д. с, вследствие чего в цепи катушки электрическое сопротивление R как бы увеличивается на значение B²l²/z_M , называемое вносимым электрическим сопротивлением

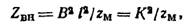(7)

где К—коэффициент электромеханической связи.

Вносимое сопротивление обратно пропорционально механическому сопротивлению. Например, если механическое сопротивление катушки равно бесконечности, то вносимое сопротивление равно нулю. Это становится понятным, если учесть, что при бесконечно большом механическом сопротивлении катушка находится в покое, и, следовательно, в витках ее не возбуждается противо- э. д. с.

Итак, сопротивление, вносимое из механической системы в электрическую цепь или из электрической цепи в механическую систему, отражает связь этих систем и их взаимодействие. Ясно, что взаимодействие это тем больше, чем больше коэффициент электромеханической связи К. Попытаемся глубже выяснить природу вносимого сопротивления. Для простоты предположим, что механическое сопротивление чисто активно (Z_M = r). Тогда (3) можно переписать в виде:

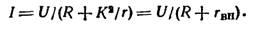(8)

Умножая обе части на I и преобразуя, получаем:

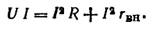(9)

Очевидно, что левая часть равенства — электрическая мощность, подводимая к катушке, а в правой части равенства — член I²R представляет собой мощность, затрачиваемую на нагрев проводника, и член 1²r_вн — часть подведенной электрической мощности, преобразованной в механическую и затраченной в механической системе на преодоление трения.

Если электрическое и механическое сопротивления реактивны, то в правой части выражения (9) получим сумму величин — кажущейся электрической мощности в катушке и кажущейся электрической мощности, перешедшей в кажущуюся механическую мощность.

Таким образом, вносимое сопротивление отображает ту часть подводимой мощности, которая преобразовывается в другой ее вид.

Аналогично могут быть получены выражения для коэффициента электромеханической связи и вносимого сопротивления для электростатического и пьезоэлектрического преобразователей.

Электростатический преобразователь состоит из неподвижной и подвижной обкладок, находящихся на расстоянии d. При приложении к ним постоянного напряжения U_o и переменного напряжения частоты ω подвижная обкладка начнет колебаться с той же частотой Коэффициент электромеханической связи будет

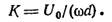(10)

Для пьезоэлектрического преобразователя с изгибной деформацией, представляющего собой пластинку длиной l и толщиной h, колеблющуюся при приложении к ней переменного напряжения частоты ω, коэффициент электромеханической связи будет

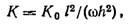
где К₀ — коэффициент пьезоэффекта.

КОЛЕБАНИЯ И ВОЛНЫ В СРЕДЕ

Рассмотрим процесс возникновения и распространения колебаний в воздушной среде.

Пусть имеется бесконечно большая жесткая стенка С, в которой может передвигаться вправо и влево относительно своего положения равновесия поршень П (рис. 4). Пусть, например, в данный момент поршень идет вправо, толкая находящиеся перед ним частицы воздуха. Частицы, отклоняясь от своего положения равновесия, в свою очередь толкают частицы, находящиеся вправо от них, т. е. следующие за ними и т. д. Справа от поршня образуется сгущение воздуха или область с повышенным атмосферным давлением. Толчки от одной частицы воздуха к другой передаются все дальше от поршня, вследствие чего вправо от него распространяется сгущение. Пусть теперь поршень после того, как он достиг своего крайнего правого положения, начал передвигаться влево. Тогда перед ним образовывается разрежение воздуха, или область с пониженным атмосферным давлением. Поскольку у поверхности поршня создалась область разрежения, туда устремятся примыкающие к ней частицы воздуха. На том месте, где они находились, в свою очередь образуется область разрежения, в которую устремятся другие, примыкающие к этой области, частицы воздуха. В результате вправо от поршня будет распространяться разрежение. Таким образом, колебания поршня периодически вызывают во внешней среде (воздухе) возмущения в виде сгущения и разрежения, причем одному периоду колебаний (движение поршня вперед и назад) соответствует одно сгущение и одно разрежение.

Давление р, измеренное в какой-то определенной точке среды, окружающей поршень, изменяется в зависимости от времени по закону, подобному закону движения поршня. При колебательном движении поршня давление в рассматриваемой точке сначала нарастает, становясь больше атмосферного давления р_о, а затем спадает до значения меньшего, чем атмосферное давление, и, наконец, опять увеличивается до значения р_о.

Графически процесс изменения давления во времени в данной точке среды изображен на рис. 5, который соответствует движению поршня, совершаемому по синусоидальному закону. Значение давления в каждый момент времени называется его мгновенным значением. Давление в каждой данной точке можно представить в виде суммы двух составляющих: постоянной, равной атмосферному давлению, и накладывающейся на него переменной. Последняя обычно называется звуковым давлением Период изменения давления Т равен периоду колебаний поршня. Амплитуда же звукового давления пропорциональна амплитуде колебаний поршня. Заметим, что на рис. 5 амплитуда звукового давления сильно преувеличена по сравнению со значением атмосферного давления из-за невозможности изобразить величины давлений в истинном соотношении, так как амплитуда звукового давления даже самых громких звуков составляет меньше одной тысячной доли от величины атмосферного давления.

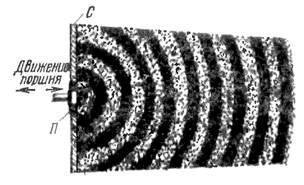
Рис. 4. Образование звуковых волн в среде

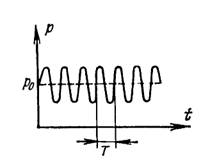
Рис. 5. Зависимость давления в среде от времени

Звуковое давление, как и всякое давление, измеряется силой, действующей на единицу площади. Поэтому в акустике за единицу звукового давления принято такое давление, при котором на площадь в 1 м² действует сила, равная 1 Н. Эта единица звукового давления называется паскаль (Па). Паскаль является удобной единицей измерения, так как в большинстве случаев значения звукового давления изменяются от сотых долей паскаля до нескольких его единиц. Звуковое давление при средней громкости разговора составляет доли паскаля. Среднее атмосферное давление, соответствующее давлению ртутного столба высотой 760 мм, составляет приблизительно 10⁵ Па.

Как и другие акустические величины, звуковое давление также измеряется в действующих значениях.

Состояние среды в рассматриваемой точке можно охарактеризовать не только изменением давления в ней, но и скоростью частиц воздуха или смещением их относительно положения равновесия. При синусоидальных колебаниях поршня кривые скорости или смещения частиц в зависимости от времени имеют также синусоидальную форму.

На рис. 6 изображено изменение во времени скорости частиц, обычно называемой в акустике колебательной скоростью. Колебательная скорость x в разные моменты времени имеет разные значения и знаки. Таким образом, в звуковом поле каждая частица среды находится в определенной фазе колебаний.

Итак, колебания источника звука (например, поршня) вызывают в среде сгущения и разрежения. Область, в которой наблюдаются сгущения и разрежения, называется звуковым полем. Сгущения и разрежения распространяются в среде с определенной скоростью, называемой скоростью распространения звука.

Ее значение зависит от характера и состояния среды. Так, скорость звука в газовой среде:

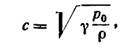(11)

где р_о — постоянное (атмосферное) давление; γ — показатель адиабаты, т.е. отношение теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме. Это отношение для воздуха равно 1,4; р — плотность воздуха, равная при 0°С и 760 мм рт. ст. 1,3 кг/м³.

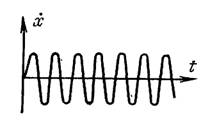
Рис. 6. Зависимость колебательной скорости в среде от времени

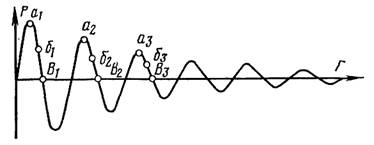
Рис. 7. Зависимость звукового давления от расстояния до источника

Для воздуха при этих условиях скорость распространения звука равна 331 м/с, а при 20° С она повышается до 344 м/с.

Скорость звука никоим образом не следует смешивать с колебательной скоростью частиц среды. Колебательная скорость частиц среды в зависимости от различных условий (например, от амплитуды, частоты колебаний источника звука) может иметь разные значения, при этом во много раз меньшие скорости распространения звука. Процессы колебаний частиц среды и распространения звука различны и по существу. В то время как звук при отсутствии препятствий может распространяться в среде сколь угодно далеко от источника, частицы среды колеблются около своего положения равновесия и поступательного движения не имеют.

Если одновременно измерить звуковое давление в различных точках прямой в направлении распространения звука, то с помощью полученных значений можно построить кривую зависимости звукового давления р от расстояния r. При синусоидальных колебаниях источника звука эта кривая имеет показанную на рис. 7 форму, также близкую к синусоиде. Правда, полученная кривая будет отличаться от идеальной синусоиды: последующие амплитуды ее уменьшаются по мере удаления от источника в результате того, что энергия звука распределяется на все большую поверхность и поглощается в самой среде.

Каждой точке, расположенной на кривой, соответствует своя фаза колебания. Однако можно указать некоторое число точек с равными фазами. Так, например, в точках а₁, а₂, а₃, имеет место максимум звукового давления. Одной и той же фазой характеризуются также колебания в точках б₁ и б₂, б₃. Какое же расстояние разделяет точки с одинаковой фазой? Известно, что за один период источник звука посылает в среду одно сгущение и одно разрежение. Рассматривая рис 7, видим, что отрезок а₁а₂ или б₁б₂ равен отрезку в₁в₂, т. е. отрезку, в котором укладывается одно разрежение и одно сгущение. Так как сгущения и разрежения перемещаются со скоростью звука, то за время Т, равное одному периоду, звуковые колебания распространяются на расстояние

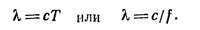(12)

Расстояние λ между самыми близкими точками (например, B₁B₂), в которых колебания находятся в одной и той же фазе, называется длиной волны. Так, для частот звука от 50 до 10 000 Гц длины волны в воздухе изменяются or 6,8 м до 3,4 см.

Разность фаз между точками, разделенными расстоянием п λ, равна 2πn, где п — целое число. Разность фаз φ между точками, находящимися на расстоянии l, может быть найдена из соотношения φ / 2π=l / λ. Отсюда

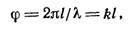(13)

где k=2π / λ =2 π f/с=ω/с.

Величина k в акустике обычно называется волновым числом. Через все точки, в которых колебания находятся в одной фазе, можно провести поверхность. Эта поверхность называется волновой или фронтом волны. В зависимости от формы, которую имеет поверхность фронта волны, различают волны сферические, плоские и т. д. Представим себе источник звука в виде пульсирующего шара, например резиновой оболочки, в которую попеременно нагнетается и из которой откачивается воздух. Такой источник звука посылает в среду сгущения и разрежения равномерно во все стороны, возбуждая сферические полны. Но на большом расстоянии от источника отдельные участки поверхности фронта сферической волны можно считать плоскими.

Практические источники звука обычно не дают ни той, ни другой формы волны в чистом виде. При возбуждении звуковых волн энергия от источника поступает в среду. Благодаря этой энергии возникают колебательные движения частиц среды. Энергия этих колебаний может передаваться телам, помещенным в звуковое поле. Энергию звукового поля можно характеризовать количеством энергии, проходящей через единицу площади, расположенной в поле перпендикулярно направлению распространения звука за единицу времени (рис. 8). Эта величина называется интенсивностью звука и измеряется в ваттах на квадратный метр.

Для сферической волны по заданной интенсивности на заданном расстоянии от источника легко определить мощность источника. Действительно, на расстоянии r от источника соответствующая сферическая поверхность равна 4πr². Если через каждый квадратный метр этой поверхности проходит мощность I, то мощность, проходящая через всю поверхность, составит 4πr²I. Эту мощность Р должен доставить источник.

Следовательно,

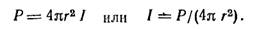(14)

Интенсивность в сферической волне обратно пропорциональна квадрату расстояния от источника. Но интенсивность связана со звуковым давлением в сферической волне соотношением I=р²/(ρс), здесь ρс — волновое или удельное акустическое сопротивление среде, представляющее собой произведение плотности среды ρ на скорость звука с в ней. Для воздуха при 20° С и 760 мм рт. ст. рс=415 кг/(с·м²).

Учитывая это, получаем: р²/(ρс)=P/(4πr²) или

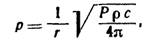(15)

т. е. звуковое давление в сферической волне обратно пропорционально расстоянию от источника звука. Звуковые давления p₁ и р₂ в точках, расположенных от источника на расстояниях r₁ и r₂, связаны соотношением p₁ / р₂ = r₂ / r₁

Рис. 8. Поток звуковой энергии через поверхность

Для плоской волны ни звуковое давление, ни интенсивность в какой-либо точке не зависят от положения точки в пространстве. Для плоской волны существуют следующие простые соотношения между звуковым давлением р, колебательной скоростью х и интенсивностью I:

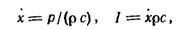(16)

где р и х могут быть выражены либо в амплитудных, либо в действующих значениях. Связь между I и р такая же, как в сферической волне.

Эти соотношения аналогичны закону Ома и зависимости мощности от тока в напряжения в электрической цепи с активным сопротивлением.

На практике при звуковом давлении l Па колебательная скорость согласно (16) будет х=1/415 = 2,4-.10~⁸ м/с. Колебательное смещение на частотах 100, 1000 и 10000 Гц согласно (2) соответственно равно: x:₁₀₀=2,4·10^-3/(2·π·100) = 3,8·10^-7 м, х₁₀₀₀=3,8·10^-7 м, х₁₀₀₀₀=3,8·10^-8 м. Амплитудные значения смещений будут в √2 больше. Ускорения на этих частотах согласно (2) х₁₀₀=2·π·100·2,4·10^-3= 1,5 м/с², х₁₀₀₀=15 м/с², х=150 м/с², т. е. будут довольны большими.

Так как значения акустических величин меняются в очень широких пределах, то их удобно выражать не в абсолютных значениях, а в логарифмических. К тому же громкость звука приближенно пропорциональна логарифму акустических величин (звукового давления, интенсивности и т. п.). Для вычисления таких логарифмических значений (уровней) пользуются следующими зависимостями.

Для звукового давления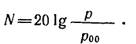

Для интенсивности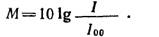

Величины N и М измеряются в децибелах (дБ). В качестве р₀₀ и I₀₀ обычно принимаются значения соответственно 2·10^-5 Па и 10^-12 Вт/м², уровень которых называется стандартным нулевым.

Уровень звукового давления в 1 Па будет равен 94 дБ.

Положим, что следует определить уровень звукового давления 2 Па:

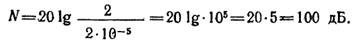
В.К. Иофе, М.В. Лизунков     

Часть [1]  [2]  [3]  [4]  [5]  [5]  [7]  [8]  [9]  [10]  [11]  [12]  [13]

Статьи

Ламповый звук Тайны лампового звука Волшебство лампового звука [1] [2] Когда лампа лучше, чем транзистор [1] [2] Почему вакуумный триод звучит музыкально Схемотехника ламповых усилителей Лампы или транзисторы? Лампы! Однотактный ламповый усилитель для начинающих Двухтактные ламповые усилители Оконечный пушпульный усилитель - схема Уильямсона-Хафлера-Кероеса Рекомендации по повторению реплики схемы Уильямсона-Хафлера-Кероеса Однотактный усилитель с непосредственной связью. Схема Loftin-White [1] [2] Трехламповый усилитель Губина Однотактник на 300В Усилители низкой частоты Расчет каскада с нагрузкой в аноде Однотактный усилитель на лампе 807 [1] [2] Циклотрон. Мощный усилитель с выходными лампами ГУ-50 SE на RB300 Однотактный усилитель мощности на 300В. Модель WE91 для 90-х годов [1] [2] Как улучшить звучание HI-FI системы [1] [2] [3] [4] [5] [6] Лампы и звук: назад, в будущее [1] [2] [3] [4] [5] Однотактный ламповый ... [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Апгрейд усилителя XD845MKIII [1] [2] "Усилитель" для наушников на SRPP [1] [2] [3] [4] [5] [6] Ламповый High-End [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [...] Обзор журнала Glass Audio за 1998 год [1] [2] Обзор журнала Glass Audio за 1999 год Корректор для винила Компенсированные регуляторы громкости Усилитель НЧ Даешь ONGAKU! Tubesaurus Rex Усилитель НЧ с комбинированной обратной связью Прибор для измерения напряжения накала высоковольтных кенотронов George Ohm живет в Харькове Ревизия однотактного усилителя с межкаскадным трансформатором Усилитель мощности НЧ с высоким КПД Двухканальный усилитель НЧ Усилитель НЧ с клавишным переключателем Радиотрансляционные установки ТУ-50 и ТУ-100 Портативный проигрыватель Усилитель НЧ Усилитель без выходного трансформатора Усилители без выходного трансформатора Лампово-полупроводниковый УМЗЧ Акустика Бытовые акустические системы [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] Там, где живут басы [1] [2] [3] [4] [5] [6] The Onken Enclosure Категории слухового восприятия [1] [2] Три взгляда на акустику помещений [1] [2] Акустика в которой мы живем [1] [2] Акустика офисов Мифы звукоизоляции Акустика отделочных материалов Акустический агрегат с объемным звучанием Акустические свойства домашней мебели Акустические линзы для громкоговорителей Акустические измерения в практике радиолюбителя Акустический фазоинвертор Акустика студий [1] [2] Полезные советы разработчиков Hi-End Триод против пентода. Что выбрать? [1] [2] SINGLE-ENDED VS PUSH-PULL [1] [2] [3] [4] [5] [6] [7] Одноламповые усилители низкой частоты Как пользоваться характеристиками электронных ламп Многоламповые усилители НЧ на импортных лампах Контактно-резисторный коммутатор входов Как проверять аппаратуру в салоне Что лучше: 4 или 8 Ом акустика? Выходной трансформатор для однотактника. Быть или не быть линейным Простая и быстрая проверка трансформаторов Десять способов усовершенствовать вашу аудиокомнату Испытатель ламп Понижение уровня фона в усилителях Evolution Пять правил рационального питания Трансформаторы в однотактных усилителях Выходные трансформаторы Измерение характеристик выходного трансформатора [1] [2] Однотактный «Magnum» Какая лампа нам нужна Какая лампа нам нужна и будет ли она? Улучшенная конфигурация листов трансформаторной стали Должен ли УМЗЧ иметь малое выходное сопротивление? [1] [2] Звук: интересные наблюдения Вся правда об акустике ProAc Немного теории лампового звука О заметности искажений История лампы 300B Краткая история возникновения Hi-Fi Возможен ли "виниловый ренессанс?" [1] [2] [3] Hi-End: Мифы и реальность [1] [2] Как не заблудиться в кабельных джунглях? Побалуйте свои уши! [1] [2] Ограничение сигнала усилителем – можно ли работать в клиппинге? "Хай-Энд" умер, да здравствует "Хай-Энд"! [1] [2] Блестящие звукозаписи [1] [2] [3] Семь слов об ошибках аудиоэкспертизы Частотные, нелинейные и фазовые искажения Внешние факторы, влияющие на восприятие звука Многоканальный окружающий звук [1] [2] [3] [4] Магнитная запись: мифы и реальность Теория схемотехники и звукотехники Для начинающих. Как работает усилитель [1] [2] Принципы схемотехники электронных ламп [1] [2] [3] [4] [5] [6] [7] [8] Хрестоматия радиолюбителя, 1963г. [1] [2] [3] [4] [5] Конструктивный расчет входных и выходных трансформаторов [1] [2] Как работают звуковые трансформаторы Элементарная теория схем с обратной связью [1] [2] [3] Теория звукотехники Двухтактно-параллельный усилитель НЧ Особенности стандартов, описывающих мощность в звукотехнике Отрицательная обратная связь в усилителях Классы усилителей мощности Элементарная теория триода [1] [2] [3] [4] [5] [6] [7] [8] [9] Как работает лучевой тетрод О мощности, ваттах, децибелах... [1] [2] Теория звука [1] [2] [3] [4] Звук и цифровые технологии [1] [2] [3] [4] [5] [6] Проектирование абсолютно устойчивых усилителей [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] Звуковые форматы Описание стандарта MP3 Правильная мощность Начинающим. Радиолампа Высококачественный усилитель низкой частоты Объемный звук [1] [2] [3] Парадоксы электрона Вибратор к гитаре Ламповый авометр Старая и популярная 12АХ7/ЕСС83 Принцип устройства и работы электро-вакуумных приборов Двухэлектродные лампы Трехэлектродные лампы Рабочий режим триода Многоэлектродные и специальные лампы Электронно-лучевые трубки Газоразрядные и индикаторные приборы Фотоэлектронные приборы Собственные шумы электронных ламп Особенности работы электронных ламп на СВЧ Специальные электронные приборы для СВЧ Надежность и испытание электровакуумных приборов Основы схемотехники ламповых усилителей Искажения в усилителях, их измерение, меры по снижению искажений Основные сведения о радиокомпонентах Источники питания Каскады усиления мощности Каскады предварительного усиления Широкополосные усилители Усилительный каскад с катодной нагрузкой [1] [2] Life in Vacuum. EL34 Life in Vacuum. 6H8C, 6H9C Life in Vacuum. SV572 SV6550 6C5C 6C3П/6C4П Двойной триод 6Н3П Пентод 6Ж5П 6П42С / 6П45С Лучевой тетрод 6П1П Пентод 6П14П в оконечном каскаде Двойной триод 6Н14П Кенотрон 1Ц11П Демпферный диод 6Ц10П Что и как мы слышим

Найти на сайте

Информация

Купить балясины и деревянные детали лестниц.

Поисковое продвижение сайтов с гарантиями.

"Интер Кредит" предлагает любой на выбор готовый бизнес в Украине: доступно и надежно.

Услуги 1С

Поход в другой мир, в мир животных, зооуголок на окраине города.

Это интересно

Для создания звукового поля источник звука — излучатель должен развивать некоторую мощность, которую он излучает. Очевидно, что для этого к источнику должна быть подведена мощность. Предположим, что источник звука представляет собой невесомый поршень, колеблющийся без трения в бесконечной стене. Если вокруг поршня создан вакуум, то ясно, что для приведения поршня в колебание достаточна бесконечно малая возбуждающая сила и соответственно такая же мощность. Однако картина резко изменится, если поршень окружает обычная среда. Оказывается, что при этом к поршню должна быть приложена определенная возбуждающая сила F, состоящая из активной и реактивной составляющих:
    Для того чтобы выяснить роли величин rR и хR, умножим обе части уравнения (17) на х. Очевидно, что в результате умножения сил на скорость мы должны получить полную мощность в левой части и в правой части — активную и реактивную ее составляющие:
    Полученное выражение аналогично, выражению для полной электрической мощности в цепи с индуктивностью и активным сопротивлением: P=I2R+jI2ωL,
    В идеальном случае неограниченной среды активная мощность х2rR идет на создание звукового поля в невозбужденных частях среды. Она теряется поршнем необратимо и должна непрерывно пополняться. Формально, поскольку процесс имеет необратимый характер, можно сказать, что мощность х2rR л затрачивается на каком-то сопротивлении rR. Сопротивление rR называют сопротивлением излучения. Таким образом, излученная источником звука мощность Р может быть выражена как
    Обычно среда, в которой происходит распространение звука, ограничена (например, поверхностями помещения, границами земной атмосферы). Казалось бы, что после возбуждения конечного объема среды источнику больше не на что затрачивать свою мощность, но необходимо помнить, что реальные среды обладают поглощением, т. е. при распространении звука часть его энергии превращается в тепло. Потери мощности имеют место также при отражении звука от ограничивающих объемов звукопоглощающих поверхностей. Поэтому при распространении звука в конечных объемах источник должен также доставлять мощность для покрытия этих потерь.
    Что касается реактивной мощности х2rR, то дело обстоит так, как будто из-за наличия среды, окружающей поршень, поршень приобрел какую-то дополнительную массу и соответственно механическое реактивное (инерционное) сопротивление. Эта проявляющаяся при колебаниях масса, обусловленная наличием среды, носит название соколеблющейся или присоединенной массы.
    Величины rR и хR не являются постоянными, а зависят от вида источника, его поверхности, от соотношения между размерами источника и длиной волны излучаемого звука, а также от удельного акустического сопротивления среды. Полное сопротивление излучения ZR может быть выражено как
    где S — поверхность источника; ρс — волновое или удельное акустическое сопротивление среды; r'r, xr — соответственно безразмерные удельные коэффициенты активного и реактивного сопротивлений, отнесенные к единице поверхности источника и к среде с единичным удельным акустическим сопротивлением.
    Значения r'r, x'r могут быть вычислены с помощью довольно сложных математических выкладок. Результаты этих вычислений для поршня, колеблющегося в бесконечной стене (рис. 9,а), изображены графически на рис. 10,а. Здесь коэффициенты rr, x'r выражены в зависимости от значения ka = 2πa/λ = 2πfa/c = ωa/c, где а — радиус поршня.
    При больших и малых значениях ka, т. е. соответственно на высоких и низких частотах, для коэффициентов r'r, x'r получаются следующие приближенные выражения: при ka << 1
    при ka >> 1 r'r =1, x'r =0.
    Коэффициент x'r определяет реактивную часть сопротивления излучения на низких частотах (при малых ka). Полное сопротивление этой части
    Оно обусловлено некоторой соколеблющейся или присоединенной массой 8/Зρа3. Поэтому величину xr иногда называют инерционной частью сопротивления излучения.
    При колебаниях поршня не в бесконечной стене возможны два случая: одна поверхность закрыта и не излучает (рис. 9,б), обе поверхности поршня открыть и излучают (рис. 9,в). Во втором случае при движении поршня, например, вправо, он создает сгущение правой стороной и разрежение — левой. Если взять какую-либо точку среды, находящуюся в плоскости поршня, то очевидно, что сгущения и разрежения доходят до нее одновременно и нейтрализуются. Следовательно, в плоскости поршня звуковое давление равно нулю. Возьмем теперь точку О, лежащую где-либо вне плоскости поршня. Пути колебаний (сгущения и разрежения) до точки О от обеих сторон поршня различаются на какую-то величину ∆l. Соответственно разность фаз φ колебаний, приходящих от обеих сторон поршня, равна уже не π, а φ = π + 2π∆l /λ.
    Член 2π∆l /λ, должен быть достаточно большим, чтобы в точке О сгущения м разрежения не нейтрализовались. На низких частотах при заданной разности путей ∆l значение 2π∆l /λ мало. Поэтому будет мало и развиваемое звуковое давление. Чтобы увеличить звуковое давление на низких частотах, необходимо поршень помещать в бесконечную стену (при этом ∆l = ∞), а практически—в экран достаточно больших размеров.
    Обычно вместо экрана применяют оформления в виде открытых с задней стороны ящиков, о чем подробнее будет сказано далее.
    В поршне с закрытой задней поверхностью, изображенном на рис. 9,6, нейтрализация звукового давления, создаваемого передней поверхностью поршня, отсутствует. Однако на низких частотах звуковое давление, создаваемое таким поршнем, меньше, чем звуковое давление, создаваемое поршнем, колеблющимся в бесконечной стене. Это происходит за счет того, что в первом случае энергия излучается в окружающую среду в пределах телесного угла 4π, в то время как во втором она излучается только в пределах угла 2π. На высоких частотах разница будет небольшой из-за направленности излучения, о чем будет сказано далее. Следовательно, для излучения звуков низких частот важно помещать поршень в большой экран.
    На рис. 10 кроме кривых rr, x'r для поршня в бесконечном экране (а) приведены кривые r'r, x'r для поршня, закрытого с одной стороны (б), и кривые r'r, x'r для поршня, открытого с двух сторон (в) Для малых значений ka аналогично (21) значения r'r соответственно равны:
    Далее...