|
Спектр звука
Спектр звукового сигнала (звуковой волны) является одним из важнейших инструментов анализа и обработки звука. Спектральное
разложение сигналов – тема обширная и сложная. Мы постараемся раскрыть эту тему, не слишком вдаваясь в ее теоретические подробности.
Французский математик Фурье (1768-1830) и его последователи доказали, что любую, обязательно периодическую функцию, в
случае ее соответствия некоторым математическим условиям можно разложить в ряд (сумму) косинусов и синусов с некоторыми коэффициентами,
называемый тригонометрическим рядом Фурье. Проводить рассмотрение сухой математики этого метода разложения
мы не будем. Скажем лишь, что, по сути, периодическая на интервале 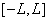 функция
f( x), задаваемая некоторым аналитическим выражением (пусть даже очень сложным) может быть по-другому записана в форме конечной
или бесконечной суммы вида:
 ,(*)
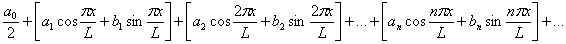где a k, b k – это так называемые коэффициенты Фурье, рассчитывающиеся по некоторой формуле. Иначе говоря,
при некоторых условиях, использование ряда Фурье (*) функции f( x) эквивалентно использованию самой функции f( x). То есть,
ряд Фурье – это как бы альтернативный способ записи функцию f( x). При этом, не смотря на то, что ряд Фурье может быть бесконечным,
предлагаемая им форма записи оказывается очень удобной при проведении анализа и обработки (о том, что это нам дает применительно
к звуковым сигналам, мы еще поговорим).
Обратим внимание, что если коэффициенты a k, b k в формуле (*) - это некоторые числа, рассчитывающиеся по специальной
формуле, то единственным изменяющимся коэффициентом при x внутри косинусов и синусов является целое число k ( k имеет значения
1, 2, 3 и т.д.). Это означает, что ряд Фурье функции f( x) можно представить графически, отложив по оси абсцисс значение
k, а по оси ординат – величины коэффициентов a k и b k (в некоторой форме).
Рассмотрим в качестве примера функцию:
 .
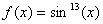График функции представлен на рис. 1.
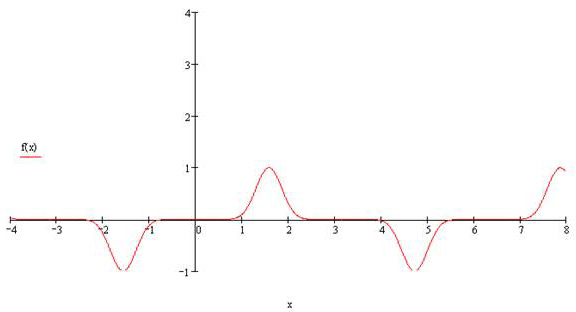
Это периодическая функция с периодом 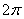 . Разложение этой функции в ряд Фурье
дает следующий результат:
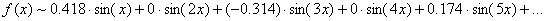
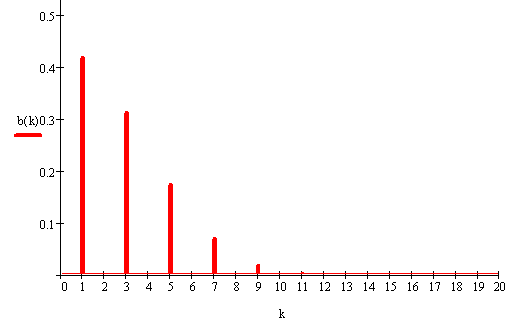
То есть, коэффициенты a k равны нулю для всех k, а коэффициенты b k не равны нулю только для нечетных k. Этот ряд Фурье
можно представить графически в виде графика, как показано на рис. 2.
Так можно поступить с периодическими функциями. Однако, как на практике, так и в теории, далеко не все функции являются
периодическими. Чтобы получить возможность раскладывать непериодическую функцию f( x) в ряд Фурье, можно воспользоваться
«хитростью». Как правило, при рассмотрении некоторой сложной непериодической функции нас не интересуют ее значения на всей
области определения; нам достаточно рассматривать функцию лишь на определенном конечном интервале [ x 1, x 2] для некоторых
x 1 и x 2. В этом случае функцию можно рассматривать как периодическую, с периодом T = x 2 – x 1. Для ее разложения в ряд
Фурье на интервале [ x 1, x 2] мы можем искусственно представить 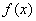 в виде некоторой
периодической функции 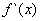 , полученной путем «зацикливания» значений функции f(
x) из рассматриваемого интервала. После этой процедуры, непериодическая функция f( x) превращается в периодическую
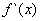, которая может быть разложена в ряд Фурье.
До сих пор мы говорили о математике. Как же все сказанное соотносится с практикой? Действительно, рассмотренный нами
способ разложения в ряд Фурье работает для функций, записанных в виде аналитических выражений. К сожалению, на практике записать
функцию в виде аналитического выражения возможно лишь в единичных случаях. В реальности чаще всего приходится работать с
изменяющимися во времени величинами, никак неподдающимися аналитической записи. Кроме того, значения анализируемой величины
чаще всего известны не в любой момент времени, а лишь тогда, когда производится их регистрация (иными словами, значения анализируемой
величины дискретны). В частности, интересующие нас сейчас реальные звуковые колебания, являются как раз
такой величиной. Оказывается, к таким величинам тоже может быть применена вариация анализа Фурье. Для разложения в ряд Фурье
сигналов, описанных их дискретными значениями, применяют Дискретное Преобразование Фурье (ДПФ
) – специально созданная разновидность анализа Фурье. Алгоритм ДПФ был адаптирован для применения в цифровой вычислительной
технике и ускорен, в результате чего появился еще один алгоритм, названный Быстрое Преобразование Фурье
- БПФ ( Fast Fourier Transform - FFT). БПФ очень широко
используется буквально во всех областях науки и техники.
Используя ДПФ/БПФ, звуковой сигнал, описанный его численными значениями, подобно математической функции, может представить
в виде спектра входящих в него частот (частотный спектр). Частотные составляющие
спектра - это синусоидальные колебания (так называемые чистые тона), каждое из которых имеет свою собственную
амплитуду, частоту и фазу. В формуле (*) коэффициенты a k и b k пр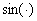и  и
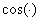 показывают амплитуду соответствующей частотной составляющей, а  –
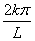ее частоту. Любое, даже самое сложное по форме колебание (например, звук голоса человека), можно представить в виде суммы
простейших синусоидальных колебаний определенных частот и амплитуд. На рис. 3 представлен график реальной звуковой волны.
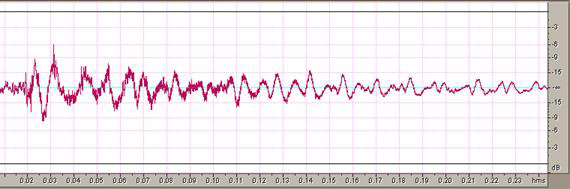
На графике по оси абсцисс откладывается время, а по оси ординат - амплитуда волны (измеренная в децибелах). Спектр этого
звукового сигнала представлен в виде графика на рис. 4.
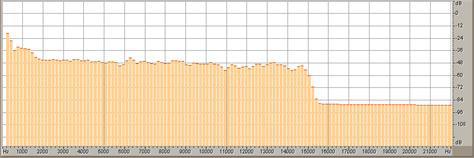
На графике спектра по оси абсцисс откладывается частота спектральных составляющих (измеренная в Гц), а по оси ординат
– амплитуда этих спектральных составляющих.
Обратим внимание на один очень важный момент: даже самую сложную зависимость (функцию) спектральное разложение превращает
в некоторый математический ряд строго определенного вида (ряд может быть конечным и бесконечным). Таким образом, спектральное
разложение как бы преобразует график в график: график функции превращается в график спектра функции. А что, если наша функция
– это звуковой сигнал некоторой длительности? Выходит, что в результате спектрального преобразования он тоже превратится
в статичную картинку спектра; таким образом, информация о временных изменениях будет утеряна – перед нами будет
единый статичный спектр всего сигнала. Как же проследить динамику изменения спектра сигнала во времени?
Чтобы получить представление об изменении спектра во времени, аудио сигнал необходимо анализировать не целиком, а по
частям (говорят «блоками» или «окнами»). Например, трехсекундный аудио сигнал можно разбить
на 30 блоков. Вычислив спектр для каждого из них, мы сможем проследить динамику развития спектрального состава звучания с
разрешением 1/10 секунды. Нужно учитывать, однако, что чем меньше анализируемый блок сигнала, тем менее точен (менее информативен)
спектр этого блока. Таким образом, при проведении спектрального анализа мы сталкиваемся с дилеммой, решение которой строго
индивидуально для каждого конкретного случая. Стремясь получить высокое временное разрешение, с тем, чтобы суметь
распознать изменения спектра сигнала в динамике, мы «дробим» анализируемый сигнал на большое количество блоков, но при этом
для каждого получаем огрубленный спектр. И наоборот, стремясь получить как можно более точный и ясный спектр, нам приходится
жертвовать временным разрешением и делить сигнал на меньшее количество блоков. Эта дилемма называется принципом
неопределенности спектрального анализа.
Часть [1]
[2]
[3]
[4]
[5]
[6]
|
